




Next: Normal equations
Up: MULTIVARIATE LEAST SQUARES
Previous: MULTIVARIATE LEAST SQUARES
Let us take up a simple example
of time-series analysis.
Given the input, say 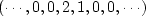 , to some filter,
say
, to some filter,
say 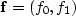 , then the output is necessarily
, then the output is necessarily
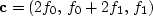 .
To design an inverse filter,
we would wish to have boldc
come out as close as possible to (1, 0, 0).
So the statement of wishes (17) is
.
To design an inverse filter,
we would wish to have boldc
come out as close as possible to (1, 0, 0).
So the statement of wishes (17) is
| ![\begin{displaymath}
\left[
\begin{array}
{c}
1 \
0 \
0 \end{array} \ri...
...\; \left[
\begin{array}
{c}
f_0 \
f_1 \end{array} \right]\end{displaymath}](img41.gif) |
(19) |
The method of solution is to premultiply by
the matrix 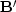 , getting
, getting
| ![\begin{displaymath}
\left[
\begin{array}
{ccc}
2 & 1 & 0 \ 0 & 2 & 1 \end{ar...
...
\left[
\begin{array}
{ccc}
f_0 \ f_1 \end{array} \right] \end{displaymath}](img42.gif) |
(20) |
Thus,
| ![\begin{displaymath}
\left[
\begin{array}
{c}
2 \ 0 \end{array} \right]
\eq
...
...
\; \left[
\begin{array}
{c}
f_0 \ f_1 \end{array} \right] \end{displaymath}](img43.gif) |
(21) |
and the inverse filter comes out to be
| ![\begin{displaymath}
\left[
\begin{array}
{c}
f_0 \ f_1 \end{array} \right]
...
...rray}
{r}
{10 \over 21} \ -{4 \over 21} \end{array} \right] \end{displaymath}](img44.gif) |
(22) |
Inserting this value of (f0,f1) back into (19)
yields the actual output
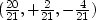 ,which is not a bad approximation to (1, 0, 0).
,which is not a bad approximation to (1, 0, 0).





Next: Normal equations
Up: MULTIVARIATE LEAST SQUARES
Previous: MULTIVARIATE LEAST SQUARES
Stanford Exploration Project
10/21/1998
![\begin{displaymath}
\left[
\begin{array}
{c}
1 \
0 \
0 \end{array} \ri...
...\; \left[
\begin{array}
{c}
f_0 \
f_1 \end{array} \right]\end{displaymath}](img41.gif)
![\begin{displaymath}
\left[
\begin{array}
{c}
1 \
0 \
0 \end{array} \ri...
...\; \left[
\begin{array}
{c}
f_0 \
f_1 \end{array} \right]\end{displaymath}](img41.gif)
![\begin{displaymath}
\left[
\begin{array}
{ccc}
2 & 1 & 0 \ 0 & 2 & 1 \end{ar...
...
\left[
\begin{array}
{ccc}
f_0 \ f_1 \end{array} \right] \end{displaymath}](img42.gif)