




Next: Inverse filter example
Up: Model fitting by least
Previous: Model fitting by least
As described at the beginning of chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
signals and images will be specified here
by numbers packed into abstract vectors.
We consider first a hypothetical application
with one data vector
,
signals and images will be specified here
by numbers packed into abstract vectors.
We consider first a hypothetical application
with one data vector 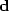 and two
fitting vectors
and two
fitting vectors 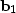 and
and 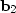 .Each fitting vector is also known as a ``regressor."
Our first task is to try to approximate the data vector
.Each fitting vector is also known as a ``regressor."
Our first task is to try to approximate the data vector 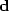 by a scaled combination of the two regressor vectors.
The scale factors x1 and x2
should be chosen so that the model matches the data, i.e.,
by a scaled combination of the two regressor vectors.
The scale factors x1 and x2
should be chosen so that the model matches the data, i.e.,
| 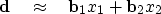 |
(1) |
For example,
if I print the characters ``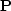 '' and ``
'' and ``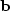 ''
on top of each other,
I get ``
''
on top of each other,
I get ``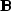 ,'' which looks something like
an image of the letter ``
,'' which looks something like
an image of the letter ``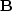 .''
This is analogous to
.''
This is analogous to 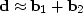 .More realistically,
.More realistically, 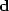 could contain a sawtooth function of time,
and
could contain a sawtooth function of time,
and 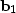 and
and 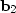 could be sinusoids.
Still more realistically,
could be sinusoids.
Still more realistically,
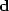 could be an observed 2-D wave field, and
could be an observed 2-D wave field, and
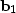 and
and
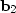 could be theoretical data in two parts,
where the contribution of each part is to be learned by fitting.
(One part could be primary reflections and the other multiple reflections.)
could be theoretical data in two parts,
where the contribution of each part is to be learned by fitting.
(One part could be primary reflections and the other multiple reflections.)
Notice that we could take the partial derivative
of the data in (1) with respect to an unknown,
say x1,
and the result is the regressor 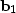 .
.
|
The partial derivative of all data
with respect to any model parameter
gives a regressor.
A regressor is a column in the partial-derivative matrix.
|
Equation (1) is often expressed in the more compact
mathematical matrix notation 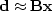 ,but in our derivation here
we will keep track of each component explicitly
and use mathematical matrix notation to summarize the final result.
Fitting the data
,but in our derivation here
we will keep track of each component explicitly
and use mathematical matrix notation to summarize the final result.
Fitting the data 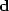 to its two theoretical components
can be expressed as
minimizing the length of the residual vector
to its two theoretical components
can be expressed as
minimizing the length of the residual vector  , where
, where
| 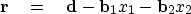 |
(2) |
So we construct a sum of squares (also called a ``quadratic form")
of the components of the residual vector by using a dot product:
| 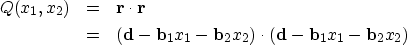 |
(3) |
| (4) |
The gradient of Q(x1,x2)/2 is defined by its two components:
| 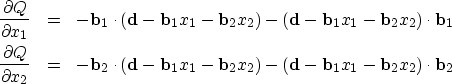 |
(5) |
| (6) |
Setting these derivatives to zero and using
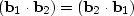 etc.,
we get
etc.,
we get
| 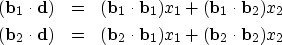 |
(7) |
| (8) |
which two equations we can use to solve for
the two unknowns x1 and x2.
Writing this expression in matrix notation, we have
| ![\begin{displaymath}
\left[
\begin{array}
{c}
({\bf b}_1 \cdot {\bf d}) \
(...
...\; \left[
\begin{array}
{c}
x_1 \
x_2 \end{array} \right]\end{displaymath}](img18.gif) |
(9) |
It is customary to use matrix notation without dot products.
For this we need some additional definitions.
To clarify these definitions, I choose the
number of components in the vectors 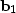 ,
, 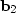 , and
, and 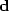 to be three.
Thus I can explicitly write a matrix boldB in full as
to be three.
Thus I can explicitly write a matrix boldB in full as
| ![\begin{displaymath}
\bold B \eq [ {\bf b}_1 \quad {\bf b}_2 ] \eq
\left[
\begi...
...2} \ b_{21} & b_{22} \ b_{31} & b_{32} \end{array} \right] \end{displaymath}](img21.gif) |
(10) |
Likewise, the transposed matrix 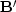 is defined by
is defined by
| ![\begin{displaymath}
\bold B' \eq
\left[
\begin{array}
{ccc}
b_{11} & b_{21} & b_{31} \ b_{12} & b_{22} & b_{32} \end{array} \right] \end{displaymath}](img23.gif) |
(11) |
The matrix in equation (9)
contains dot products.
Matrix multiplication is an abstract way of representing the dot products:
| ![\begin{displaymath}
\left[
\begin{array}
{ccc}
({\bf b}_1 \cdot {\bf b}_1) & (...
...12} \ b_{21} & b_{22} \ b_{31} & b_{32} \end{array} \right]\end{displaymath}](img24.gif) |
(12) |
Thus, equation (9) without dot products is
| ![\begin{displaymath}
\left[
\begin{array}
{ccc}
b_{11} & b_{21} & b_{31} \ b_...
...
\left[
\begin{array}
{ccc}
x_1 \ x_2 \end{array} \right] \end{displaymath}](img25.gif) |
(13) |
which has the matrix abbreviation
| 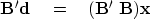 |
(14) |
Equation
(14)
is the classic result of least-squares
fitting of data to a collection of regressors.
Obviously, the same matrix form applies when there are more than
two regressors and each vector has more than three components.
Equation
(14)
leads to an analytic solution for  using an inverse matrix.
To solve formally for the unknown
using an inverse matrix.
To solve formally for the unknown  ,we premultiply by the inverse matrix
,we premultiply by the inverse matrix 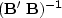 :
:
|
| 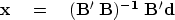 |
(15) |
Equation (15) is the central result of
least-squares
analysis.
We see it everywhere.
|
Equation (12) is an example
of what is called a ``covariance matrix.''
Such matrices usually need to be inverted,
and in equation (15)
you already see an example of the occurrence
of an inverse covariance matrix.
Any description of an application of least-squares fitting
will generally include some discussion of the covariance matrix--how
it will be computed, assumed, or estimated,
and how its inverse will be found or approximated.
In chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we found the need to weight residuals
by the inverse of their scale.
That was our first example of the occurrence
of an inverse covariance matrix--although
in that case the matrix size was only
we found the need to weight residuals
by the inverse of their scale.
That was our first example of the occurrence
of an inverse covariance matrix--although
in that case the matrix size was only 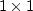 .
.
In our first manipulation of matrix algebra,
we move around some parentheses in
(14):
| 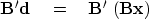 |
(16) |
Moving the parentheses implies a regrouping of terms
or a reordering of a computation.
You can verify the validity of moving the parentheses by
writing (16)
in full as the set of two equations it represents.
Equation
(14)
led to the ``analytic'' solution (15).
In a later section on conjugate gradients,
we will see that equation
(16)
expresses better than
(15)
the philosophy of computation.
Notice how equation
(16)
invites us to cancel the matrix
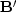 from each side.
We cannot do that of course, because
from each side.
We cannot do that of course, because
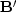 is not a number, nor is it a square matrix with an inverse.
If you really want to cancel the matrix
is not a number, nor is it a square matrix with an inverse.
If you really want to cancel the matrix 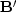 , you may,
but the equation is then only an approximation
that restates our original goal (1):
, you may,
but the equation is then only an approximation
that restates our original goal (1):
| 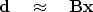 |
(17) |
A speedy problem solver might
ignore the mathematics covering the previous page,
study his or her application until he or she
is able to write the statement of wishes
(17) = (1),
premultiply by 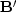 ,replace
,replace 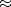 by =,
getting (14),
and take
(14)
to a simultaneous equation-solving program to get
by =,
getting (14),
and take
(14)
to a simultaneous equation-solving program to get  .
.
The formal literature does not speak of
``statement of wishes'' but of ``regression," which is the same concept.
In a regression, there is an abstract vector called the residual
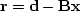 whose components should all be small.
Formally this is often written as:
whose components should all be small.
Formally this is often written as:
| 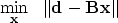 |
(18) |
The notation above with two pairs of vertical lines
looks like double absolute value,
but we can understand it as a reminder to square and sum all the components.
This notation is more explicit about what is being minimized,
but I often find myself sketching out applications
in the form of a ``statement of wishes,''
which I call a ``regression.''





Next: Inverse filter example
Up: Model fitting by least
Previous: Model fitting by least
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
signals and images will be specified here
by numbers packed into abstract vectors.
We consider first a hypothetical application
with one data vector
,
signals and images will be specified here
by numbers packed into abstract vectors.
We consider first a hypothetical application
with one data vector ![]() .
.![]() ,but in our derivation here
we will keep track of each component explicitly
and use mathematical matrix notation to summarize the final result.
Fitting the data
,but in our derivation here
we will keep track of each component explicitly
and use mathematical matrix notation to summarize the final result.
Fitting the data ![]() to its two theoretical components
can be expressed as
minimizing the length of the residual vector
to its two theoretical components
can be expressed as
minimizing the length of the residual vector ![]() , where
, where
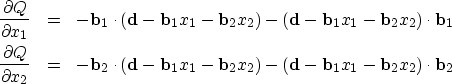
![\begin{displaymath}
\bold B \eq [ {\bf b}_1 \quad {\bf b}_2 ] \eq
\left[
\begi...
...2} \ b_{21} & b_{22} \ b_{31} & b_{32} \end{array} \right] \end{displaymath}](img21.gif)
![\begin{displaymath}
\left[
\begin{array}
{ccc}
({\bf b}_1 \cdot {\bf b}_1) & (...
...12} \ b_{21} & b_{22} \ b_{31} & b_{32} \end{array} \right]\end{displaymath}](img24.gif)
![\begin{displaymath}
\left[
\begin{array}
{ccc}
b_{11} & b_{21} & b_{31} \ b_...
...
\left[
\begin{array}
{ccc}
x_1 \ x_2 \end{array} \right] \end{displaymath}](img25.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we found the need to weight residuals
by the inverse of their scale.
That was our first example of the occurrence
of an inverse covariance matrix--although
in that case the matrix size was only
we found the need to weight residuals
by the inverse of their scale.
That was our first example of the occurrence
of an inverse covariance matrix--although
in that case the matrix size was only ![]() .
.![]() from each side.
We cannot do that of course, because
from each side.
We cannot do that of course, because
![]() is not a number, nor is it a square matrix with an inverse.
If you really want to cancel the matrix
is not a number, nor is it a square matrix with an inverse.
If you really want to cancel the matrix ![]() , you may,
but the equation is then only an approximation
that restates our original goal (1):
, you may,
but the equation is then only an approximation
that restates our original goal (1):
![]() ,replace
,replace ![]() by =,
getting (14),
and take
(14)
to a simultaneous equation-solving program to get
by =,
getting (14),
and take
(14)
to a simultaneous equation-solving program to get ![]() .
.![]() whose components should all be small.
Formally this is often written as:
whose components should all be small.
Formally this is often written as: