




Next: INVERSE NMO STACK
Up: ITERATIVE METHODS
Previous: First conjugate-gradient program
Like steepest descent,
CG methods can be accelerated if a nonsingular matrix 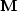 with known inverse can be found to approximate
with known inverse can be found to approximate 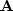 .Then,
instead of solving
.Then,
instead of solving
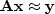 ,we solve
,we solve
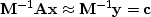 ,which should converge much faster since
,which should converge much faster since
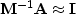 .This is called ``preconditioning.''
.This is called ``preconditioning.''
In my experience the matrix 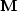 is rarely available,
except in the crude approximation of scaling columns,
so the unknowns have about equal magnitude.
As with signals and images,
spectral balancing should be helpful.
is rarely available,
except in the crude approximation of scaling columns,
so the unknowns have about equal magnitude.
As with signals and images,
spectral balancing should be helpful.
EXERCISES:
-
Remove lines from the conjugate-gradient program
to convert it to a program that solves simultaneous
equations by the method of steepest descent.
Per iteration, how many dot products are saved,
and how much is the memory requirement reduced?
-
A precision problem can arise with the CG method when many iterations
are required.
What happens is that R drifts away from
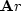 and X drifts away from
and X drifts away from 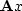 .Revise the program cgmeth() to restore consistency
every twentieth iteration.
.Revise the program cgmeth() to restore consistency
every twentieth iteration.





Next: INVERSE NMO STACK
Up: ITERATIVE METHODS
Previous: First conjugate-gradient program
Stanford Exploration Project
10/21/1998
![]() is rarely available,
except in the crude approximation of scaling columns,
so the unknowns have about equal magnitude.
As with signals and images,
spectral balancing should be helpful.
is rarely available,
except in the crude approximation of scaling columns,
so the unknowns have about equal magnitude.
As with signals and images,
spectral balancing should be helpful.