




Next: First conjugate-gradient program
Up: ITERATIVE METHODS
Previous: Magic
Define the solution, the solution step (from one iteration to the next),
and the gradient by
| 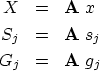 |
(39) |
| (40) |
| (41) |
A linear combination in solution space,
say s+g, corresponds to S+G in the conjugate space,
because 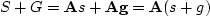 .According to equation
(31),
the residual is
.According to equation
(31),
the residual is
| 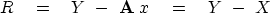 |
(42) |
The solution x is obtained by a succession of steps sj, say
| 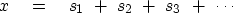 |
(43) |
The last stage of each iteration is to update the solution and the residual:
solution update: 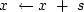 residual update:
residual update: 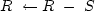
The gradient vector g is a vector with the same number
of components as the solution vector x.
A vector with this number of components is
| 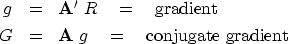 |
(44) |
| (45) |
The gradient g in the transformed space is G,
also known as the ``conjugate gradient.''
The minimization (35) is now generalized
to scan not only the line with  ,but simultaneously another line with
,but simultaneously another line with 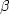 .The combination of the two lines is a plane:
.The combination of the two lines is a plane:
| 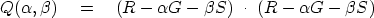 |
(46) |
The minimum is found at 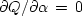 and
and
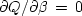 , namely,
, namely,
| 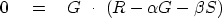 |
(47) |
| 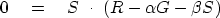 |
(48) |
The solution is
| ![\begin{displaymath}
\left[
\begin{array}
{c}
\alpha \
\beta \end{array} \r...
...begin{array}
{c}
(G\cdot R) \ (S\cdot R) \end{array} \right]\end{displaymath}](img124.gif) |
(49) |





Next: First conjugate-gradient program
Up: ITERATIVE METHODS
Previous: Magic
Stanford Exploration Project
10/21/1998
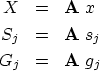
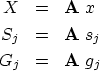
residual update:
![]() ,but simultaneously another line with
,but simultaneously another line with ![]() .The combination of the two lines is a plane:
.The combination of the two lines is a plane: