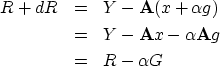Next: Conditioning the gradient
Up: ITERATIVE METHODS
Previous: ITERATIVE METHODS
Let us minimize the sum of the squares of the components
of the residual vector given by
| 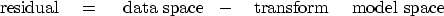 |
(30) |
| ![\begin{displaymath}
\left[
\matrix { \matrix { \cr \cr R \cr \cr \cr } }
\right]...
...\ \ \
\left[
\matrix {
\matrix { \cr x \cr \cr }
}
\right]\end{displaymath}](img96.gif) |
(31) |
Fourier-transformed variables are often capitalized.
Here we capitalize vectors transformed by the 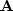 matrix.
A matrix such as
matrix.
A matrix such as 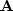 is denoted by boldface print.
is denoted by boldface print.
A contour plot is based on an altitude function of space.
The altitude is the dot product 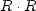 .By finding the lowest altitude
we are driving the residual vector R as close as we can to zero.
If the residual vector R reaches zero, then we have solved
the simultaneous equations
.By finding the lowest altitude
we are driving the residual vector R as close as we can to zero.
If the residual vector R reaches zero, then we have solved
the simultaneous equations 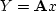 .In a two-dimensional world the vector x has two components,
(x1 , x2 ).
A contour is a curve of constant
.In a two-dimensional world the vector x has two components,
(x1 , x2 ).
A contour is a curve of constant 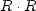 in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), given measurement errors in Y.
in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), given measurement errors in Y.
Starting from 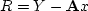 , let us see how a random search
direction can be used to try to reduce the residual.
Let g be an abstract vector with the same number of components as
the solution x,
and let g contain arbitrary or random numbers.
Let us add an unknown quantity
, let us see how a random search
direction can be used to try to reduce the residual.
Let g be an abstract vector with the same number of components as
the solution x,
and let g contain arbitrary or random numbers.
Let us add an unknown quantity  of vector g to vector x,
thereby changing x to
of vector g to vector x,
thereby changing x to 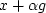 .The new residual R+dR becomes
.The new residual R+dR becomes
| 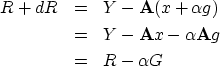 |
(32) |
| (33) |
| (34) |
We seek to minimize the dot product
| 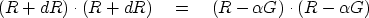 |
(35) |
Setting to zero the derivative with respect to  gives
gives
| 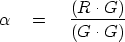 |
(36) |
Geometrically and algebraically
the new residual 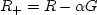 is
perpendicular to the ``fitting function'' G.
(We confirm this by substitution leading to
is
perpendicular to the ``fitting function'' G.
(We confirm this by substitution leading to 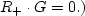
In practice, random directions are rarely used.
It is more common to use the gradient vector.
Notice also that a vector of the size of x is
| 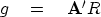 |
(37) |
Notice also that this vector can be found by taking the gradient
of the size of the residuals:
| 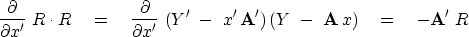 |
(38) |
Descending by use of the gradient vector is called
``the method of steepest descent."





Next: Conditioning the gradient
Up: ITERATIVE METHODS
Previous: ITERATIVE METHODS
Stanford Exploration Project
10/21/1998
![\begin{displaymath}
\left[
\matrix { \matrix { \cr \cr R \cr \cr \cr } }
\right]...
...\ \ \
\left[
\matrix {
\matrix { \cr x \cr \cr }
}
\right]\end{displaymath}](img96.gif)
![]() .By finding the lowest altitude
we are driving the residual vector R as close as we can to zero.
If the residual vector R reaches zero, then we have solved
the simultaneous equations
.By finding the lowest altitude
we are driving the residual vector R as close as we can to zero.
If the residual vector R reaches zero, then we have solved
the simultaneous equations ![]() .In a two-dimensional world the vector x has two components,
(x1 , x2 ).
A contour is a curve of constant
.In a two-dimensional world the vector x has two components,
(x1 , x2 ).
A contour is a curve of constant ![]() in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), given measurement errors in Y.
in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), given measurement errors in Y.
![]() , let us see how a random search
direction can be used to try to reduce the residual.
Let g be an abstract vector with the same number of components as
the solution x,
and let g contain arbitrary or random numbers.
Let us add an unknown quantity
, let us see how a random search
direction can be used to try to reduce the residual.
Let g be an abstract vector with the same number of components as
the solution x,
and let g contain arbitrary or random numbers.
Let us add an unknown quantity ![]() of vector g to vector x,
thereby changing x to
of vector g to vector x,
thereby changing x to ![]() .The new residual R+dR becomes
.The new residual R+dR becomes