




Next: The Nyquist frequency
Up: Discrete Fourier transform
Previous: Discrete Fourier transform
A Fourier sum may be written
| 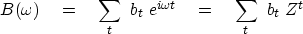 |
(1) |
where the complex value Z
is related to the real frequency
 by
by 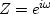 .This Fourier sum is a way of building
a continuous function of
.This Fourier sum is a way of building
a continuous function of  from discrete signal values bt in the time domain.
In this chapter we will study the computational tricks
associated with specifying both time and frequency domains
by a set of points.
Begin with an example of a signal
that is nonzero at four successive instants,
( b0, b1, b2, b3).
The transform is
from discrete signal values bt in the time domain.
In this chapter we will study the computational tricks
associated with specifying both time and frequency domains
by a set of points.
Begin with an example of a signal
that is nonzero at four successive instants,
( b0, b1, b2, b3).
The transform is
| 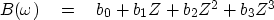 |
(2) |
The evaluation of this polynomial can be organized as a matrix times a vector,
such as
| ![\begin{displaymath}
\left[ \begin{array}
{c}
B_0 \ B_1 \ B_2 \ B_3 \end{a...
...gin{array}
{c}
b_0 \ b_1 \ b_2 \ b_3 \end{array} \right]\end{displaymath}](img5.gif) |
(3) |
Observe that the top row of the matrix evaluates the polynomial at Z=1,
a point where also
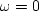 .The second row evaluates
.The second row evaluates 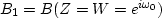 ,where
,where 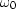 is some base frequency.
The third row evaluates the Fourier transform for
is some base frequency.
The third row evaluates the Fourier transform for 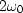 ,and the bottom row for
,and the bottom row for 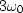 .The matrix could have more than four rows for more frequencies
and more columns for more time points.
I have made the matrix square in order to show you next
how we can find the inverse matrix.
The size of the matrix in (3) is N=4.
If we choose the base frequency
.The matrix could have more than four rows for more frequencies
and more columns for more time points.
I have made the matrix square in order to show you next
how we can find the inverse matrix.
The size of the matrix in (3) is N=4.
If we choose the base frequency 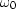 and hence W correctly,
the inverse matrix will be
and hence W correctly,
the inverse matrix will be
| ![\begin{displaymath}
\left[ \begin{array}
{c}
b_0 \ b_1 \ b_2 \ b_3 \end{a...
...gin{array}
{c}
B_0 \ B_1 \ B_2 \ B_3 \end{array} \right]\end{displaymath}](img11.gif) |
(4) |
Multiplying the matrix of
(4) with that of
(3),
we first see that the diagonals are +1 as desired.
To have the off diagonals vanish,
we need various sums,
such as 1+W +W2+W3
and 1+W2+W4+W6, to vanish.
Every element (W6, for example,
or 1/W9) is a unit vector in the complex plane.
In order for the sums of the unit vectors to vanish,
we must ensure that the vectors pull symmetrically away from the origin.
A uniform distribution of directions meets this requirement.
In other words, W should be the N-th root of unity, i.e.,
| ![\begin{displaymath}
W \eq
\sqrt[N]{1} \eq
e^{2\pi i/N}\end{displaymath}](img12.gif) |
(5) |
The lowest frequency is zero, corresponding to the top row of
(3).
The next-to-the-lowest frequency we find by setting W in
(5) to 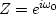 .So
.So 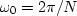 ; and
for (4) to be inverse to (3),
the frequencies required are
; and
for (4) to be inverse to (3),
the frequencies required are
| 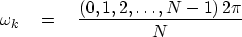 |
(6) |





Next: The Nyquist frequency
Up: Discrete Fourier transform
Previous: Discrete Fourier transform
Stanford Exploration Project
10/21/1998
![\begin{displaymath}
\left[ \begin{array}
{c}
B_0 \ B_1 \ B_2 \ B_3 \end{a...
...gin{array}
{c}
b_0 \ b_1 \ b_2 \ b_3 \end{array} \right]\end{displaymath}](img5.gif)
![\begin{displaymath}
\left[ \begin{array}
{c}
b_0 \ b_1 \ b_2 \ b_3 \end{a...
...gin{array}
{c}
B_0 \ B_1 \ B_2 \ B_3 \end{array} \right]\end{displaymath}](img11.gif)
![]() .So
.So ![]() ; and
for (4) to be inverse to (3),
the frequencies required are
; and
for (4) to be inverse to (3),
the frequencies required are