




Next: Interpretation of the modulated
Up: RETARDED COORDINATES
Previous: The chain rule and
Given a pressure field P(t,x,z), we may Fourier transform it
with respect to any or all of its independent variables (t,x,z).
Likewise, if the pressure field is specified in retarded coordinates, we
may Fourier transform with respect to (t' ,x' ,z' ).
Since the Fourier dual
of (t,x,z) is 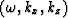 , it seems
appropriate for the dual
of (t' ,x' ,z' ) to be
, it seems
appropriate for the dual
of (t' ,x' ,z' ) to be 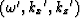 .Now the question is, how are
.Now the question is, how are 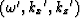 related to the familiar
related to the familiar 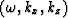 ?
The answer is contained in the chain rule for partial differentiation.
Any expression like (33)
?
The answer is contained in the chain rule for partial differentiation.
Any expression like (33)
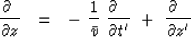
on Fourier transformation says
| 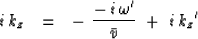 |
(36) |
Computing all the other derivatives, we
have the transformation
| 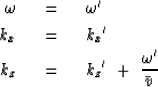 |
(37) |
| (38) |
| (39) |
Recall the dispersion relation for the scalar wave equation:
| 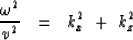 |
(40) |
Performing the substitutions from
(37),
(38) and (39) into (40) we
have the expression of the scalar wave equation
in retarded time, namely,
| 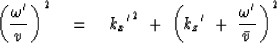 |
(41) |
These two dispersion relations are plotted in
Figure 4 for the retardation velocity
chosen equal to the medium velocity.
rdisper
Figure 4
Dispersion relation of the wave equation
in usual coordinates (left) and
retarded time coordinates (right).
|
| 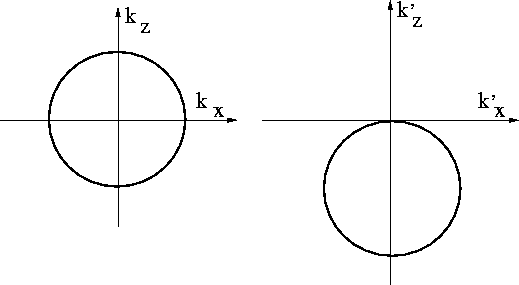 |

Figure 4 graphically illustrates that
retardation can reduce the cost of finite-difference calculations.
Waves going straight down are near the top of the dispersion curve (circle).
The effect of retardation is to shift the circle's top down to the origin.
Discretizing the x- and z-axes will cause
spatial frequency aliasing on them.
The larger the frequency 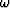 , the larger the circle.
Clearly the top of the shifted circle is further from folding.
Alternately,
, the larger the circle.
Clearly the top of the shifted circle is further from folding.
Alternately, 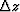 may be increased (for the sake of economy)
before k' z exceeds the Nyquist frequency
may be increased (for the sake of economy)
before k' z exceeds the Nyquist frequency 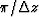 .
.





Next: Interpretation of the modulated
Up: RETARDED COORDINATES
Previous: The chain rule and
Stanford Exploration Project
10/31/1997
![]() , it seems
appropriate for the dual
of (t' ,x' ,z' ) to be
, it seems
appropriate for the dual
of (t' ,x' ,z' ) to be ![]() .Now the question is, how are
.Now the question is, how are ![]() related to the familiar
related to the familiar ![]() ?
The answer is contained in the chain rule for partial differentiation.
Any expression like (33)
?
The answer is contained in the chain rule for partial differentiation.
Any expression like (33)
![]()
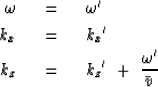
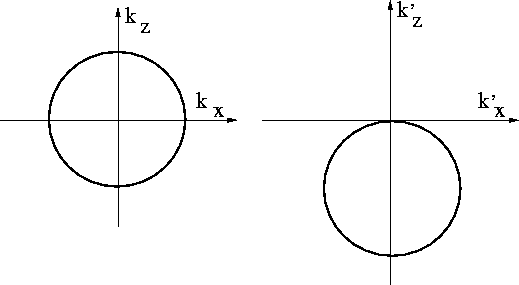
![]() , the larger the circle.
Clearly the top of the shifted circle is further from folding.
Alternately,
, the larger the circle.
Clearly the top of the shifted circle is further from folding.
Alternately, ![]() may be increased (for the sake of economy)
before k' z exceeds the Nyquist frequency
may be increased (for the sake of economy)
before k' z exceeds the Nyquist frequency ![]() .
.