Fourier analyzing the function f(x,t,z=0), seen on the earth's surface,
requires the Fourier kernel ![]() .Moving on the earth's surface at an inverse speed
of
.Moving on the earth's surface at an inverse speed
of ![]() ,the phase of the Fourier kernel, hence the kernel itself, remains constant.
Only those sinusoidal components that move at the same speed
as the Snell wave can have a nonzero correlation with it.
So if the disturbance is a single Snell wave,
then all Fourier components vanish
except for those that satisfy
,the phase of the Fourier kernel, hence the kernel itself, remains constant.
Only those sinusoidal components that move at the same speed
as the Snell wave can have a nonzero correlation with it.
So if the disturbance is a single Snell wave,
then all Fourier components vanish
except for those that satisfy ![]() .You should memorize these basic relations:
.You should memorize these basic relations:
![\begin{displaymath}
\fbox {\rule[-.4cm]{0cm}{1cm}$\displaystyle
{\strut \partia...
...{.2in}=\hspace{.2in}
\displaystyle {\strut k_x \over \omega}$}
\end{displaymath}](img123.gif) |
(51) |
In theoretical seismology a square-root function often appears as a result of using (51) to make a cosine.
Utilization of this Fourier domain interpretation
of Snell's parameter p enables us to write
the square-root equations (48),
(49) and (50) in an even more useful form.
But first the square-root equation must be reexpressed in the Fourier domain.
This is done by replacing the ![]() operator
in (48), (49) and (50)
by
operator
in (48), (49) and (50)
by ![]() .The result is
.The result is
| |
(52) |
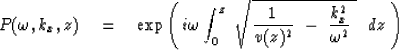 |
(53) |