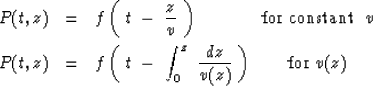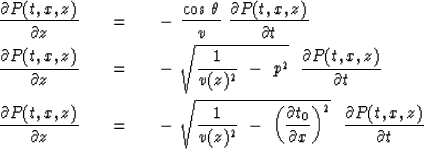Next: Fourier decomposition
Up: THE PARAXIAL WAVE EQUATION
Previous: Snell waves
An important task is to predict
the wavefield inside the earth
given the waveform at the surface.
For a downgoing plane wave this can be done by
the time-shifting partial differential equation
| 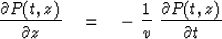 |
(43) |
as may be readily verified by substituting either of the trial solutions
| 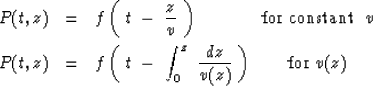 |
(44) |
| (45) |
This also works for nonvertically incident waves
with the partial differential equation
| 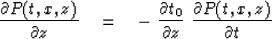 |
(46) |
which has the solution
| 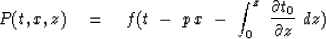 |
(47) |
In interpreting (46) and (47) recall
that 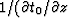 is the apparent velocity in a borehole.
The partial derivative of wavefield P(t,x,z) with respect
to depth z is taken at constant x, i.e., the
wave is extrapolated down the borehole.
The idea that downward extrapolation can
be achieved by merely time shifting holds only when a
single
Snell wave is present; that is, the
same
arbitrary time function must be seen at all locations.
is the apparent velocity in a borehole.
The partial derivative of wavefield P(t,x,z) with respect
to depth z is taken at constant x, i.e., the
wave is extrapolated down the borehole.
The idea that downward extrapolation can
be achieved by merely time shifting holds only when a
single
Snell wave is present; that is, the
same
arbitrary time function must be seen at all locations.
Substitution from (38) and (39) also enables
us to rewrite (46) in the various forms
| 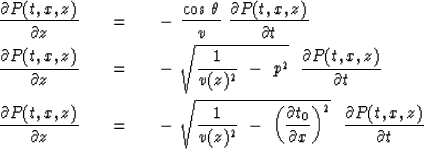 |
(48) |
| (49) |
| (50) |
Equations (48),
(49) and (50) are paraxial wave equations.
Since 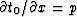 can be measured
along the surface of the earth,
it seems that equation (50),
along with an assumed velocity v(z) and some observed data P(t,x,z=0),
would enable us to determine
can be measured
along the surface of the earth,
it seems that equation (50),
along with an assumed velocity v(z) and some observed data P(t,x,z=0),
would enable us to determine 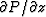 , which
is the necessary first step of downward continuation.
But the presumption was that there was only a single Snell wave
and not a superposition of several Snell waves.
Superposition of different waveforms on different Snell paths
would cause different time functions to be seen at different places.
Then a mere time shift would not achieve downward continuation.
Luckily, a complicated wavefield that is variable from place to place
may be decomposed into many Snell waves,
each of which can be downward extrapolated
with the differential equations (48),
(49) and (50) or their solution (47).
One such decomposition technique is
Fourier analysis.
, which
is the necessary first step of downward continuation.
But the presumption was that there was only a single Snell wave
and not a superposition of several Snell waves.
Superposition of different waveforms on different Snell paths
would cause different time functions to be seen at different places.
Then a mere time shift would not achieve downward continuation.
Luckily, a complicated wavefield that is variable from place to place
may be decomposed into many Snell waves,
each of which can be downward extrapolated
with the differential equations (48),
(49) and (50) or their solution (47).
One such decomposition technique is
Fourier analysis.





Next: Fourier decomposition
Up: THE PARAXIAL WAVE EQUATION
Previous: Snell waves
Stanford Exploration Project
10/31/1997