




Next: Retarded Muir recurrence
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: Lateral derivatives
The frequency 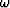 will range over
will range over 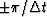 .If the t-axis is going to be handled by finite differencing
then we will need the Z-transform variable equation (50)
.If the t-axis is going to be handled by finite differencing
then we will need the Z-transform variable equation (50)
|  |
(50) |
and the causal derivative (52)
| 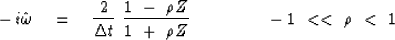 |
(51) |
The data can be subsampled or supersampled before processing,
so 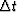 is an adjustable parameter.
The causality parameter
is an adjustable parameter.
The causality parameter 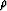 should be
a small amount less than unity,
say
should be
a small amount less than unity,
say 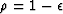 where
where 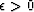 is an adjustable parameter.
You may want to introduce
is an adjustable parameter.
You may want to introduce 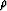 even if you are migrating
in the frequency domain because it reduces wraparound
in the time domain--it is a kind of viscosity.
The
even if you are migrating
in the frequency domain because it reduces wraparound
in the time domain--it is a kind of viscosity.
The  should be about inverse to the data length,
say 1 / Nt where Nt is the number of points on the time axis.
(Because I made many plots of synthetic hyperbolas with square root gain,
should be about inverse to the data length,
say 1 / Nt where Nt is the number of points on the time axis.
(Because I made many plots of synthetic hyperbolas with square root gain,
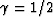 , time wraparounds were larger than life.
So I had the program default to
, time wraparounds were larger than life.
So I had the program default to  four times larger).
If you like to adjust free parameters,
you could separately adjust numerator and denominator values of
four times larger).
If you like to adjust free parameters,
you could separately adjust numerator and denominator values of 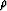 .Subsequently, I'll distinguish between
.Subsequently, I'll distinguish between 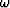 and
and 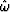 ,but you can take
,but you can take 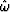 to be
to be 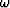 if you don't care to
introduce causality.
if you don't care to
introduce causality.





Next: Retarded Muir recurrence
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: Lateral derivatives
Stanford Exploration Project
10/31/1997
![]() will range over
will range over ![]() .If the t-axis is going to be handled by finite differencing
then we will need the Z-transform variable equation (50)
.If the t-axis is going to be handled by finite differencing
then we will need the Z-transform variable equation (50)