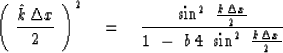Next: Viscosity and causality
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: ACCURACY THE CONTRACTOR'S VIEW
First, kx will range over 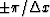 .If the x-axis is going to be handled by finite differencing
then we will need equation (39):
.If the x-axis is going to be handled by finite differencing
then we will need equation (39):
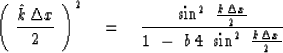
So if the x-axis is going to be handled by finite differencing then
subsequent reference to kx should be replaced by 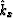 .The finite differencing introduces the free parameter b.
Likewise, you could also scale the whole expression
by an adjustable parameter near unity.
Also,
.The finite differencing introduces the free parameter b.
Likewise, you could also scale the whole expression
by an adjustable parameter near unity.
Also, 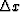 isn't necessarily fixed by the data collection.
You could always interpolate the data before processing.
A finite-difference method using interpolated data could be mandated
by enough lateral velocity variation.
isn't necessarily fixed by the data collection.
You could always interpolate the data before processing.
A finite-difference method using interpolated data could be mandated
by enough lateral velocity variation.





Next: Viscosity and causality
Up: ACCURACY THE CONTRACTOR'S VIEW
Previous: ACCURACY THE CONTRACTOR'S VIEW
Stanford Exploration Project
10/31/1997
![]() .If the x-axis is going to be handled by finite differencing
then we will need equation (39):
.If the x-axis is going to be handled by finite differencing
then we will need equation (39):