




Next: The 1/6 trick
Up: FREQUENCY DISPERSION IN WAVE-MIGRATION
Previous: Spatial aliasing various space
The defining equation for a second
difference
operator is
| 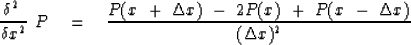 |
(30) |
The second
derivative
operator is defined by taking the limit
| 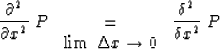 |
(31) |
Many different definitions can all go to the same limit
as 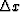 goes to zero.
The problem is to find an expression that is accurate when
goes to zero.
The problem is to find an expression that is accurate when 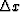 is
larger than zero and, on a practical level,
is not too complicated.
Our first objective is to see how the accuracy of
equation (30) can be evaluated quantitatively.
Second, we will look at an expression that is slightly more complicated
than (30) but much more accurate.
is
larger than zero and, on a practical level,
is not too complicated.
Our first objective is to see how the accuracy of
equation (30) can be evaluated quantitatively.
Second, we will look at an expression that is slightly more complicated
than (30) but much more accurate.
The basic method of analysis we will use is Fourier transformation.
Take the derivatives of
the complex exponential 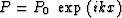 and
look at any errors as functions of the spatial frequency k.
For the second derivative,
and
look at any errors as functions of the spatial frequency k.
For the second derivative,
| 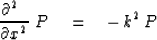 |
(32) |
Define 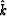 by an expression analogous to the difference
operator:
by an expression analogous to the difference
operator:
| 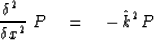 |
(33) |
Ideally 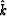 would equal k.
Inserting
the complex exponential
would equal k.
Inserting
the complex exponential 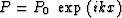 into (30),
we see that the definition (33)
gives an expression for
into (30),
we see that the definition (33)
gives an expression for 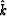 in terms of k:
in terms of k:
| ![\begin{displaymath}
- \hat k^2 P \eq {P_0 \over \Delta x^2 } \
\left[ \ e^{ik(x+\Delta x)}\ -\ 2\,e^{ikx} + e^{ik( x - \Delta x )} \right]\end{displaymath}](img106.gif) |
(34) |
| ![\begin{displaymath}
-\ { \delta^2 \ \over \delta x^2 }
\eq
\hat k^2 \eq {2 \over \Delta x^2 } \
[ 1 \ -\ \cos (k \Delta x ) ]\end{displaymath}](img107.gif) |
(35) |
It is a straightforward matter
to make plots of 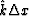 versus
versus  from (35).
The half-angle trig formula allows us to take an
analytic square root of (35), which is
from (35).
The half-angle trig formula allows us to take an
analytic square root of (35), which is
| 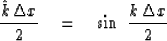 |
(36) |
Series expansion shows that for low frequencies 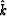 is
a good approximation to k.
At the Nyquist frequency,
defined by
is
a good approximation to k.
At the Nyquist frequency,
defined by 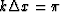 ,the approximation
,the approximation 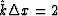 is a poor approximation to
is a poor approximation to  .
.





Next: The 1/6 trick
Up: FREQUENCY DISPERSION IN WAVE-MIGRATION
Previous: Spatial aliasing various space
Stanford Exploration Project
10/31/1997
![]() and
look at any errors as functions of the spatial frequency k.
For the second derivative,
and
look at any errors as functions of the spatial frequency k.
For the second derivative,