Aliasing can occur on the axes of time, depth, geophone, shot, midpoint,
offset, or crossline.
In practice, aliasing is the worst on the horizontal space axes.
Figure 19 provides an illustration.
Looking at that figure,
you get confused about whether the dip is to the left or right.
Mathematical analysis has the same difficulty.
The dispersion relation of the wave equation enables us to compute the
vertical spatial frequency kz from the temporal frequency ![]() ,the velocity v, and the horizontal spatial frequency kx using the
semicircle relation
,the velocity v, and the horizontal spatial frequency kx using the
semicircle relation ![]()
![]() .Sampling on the x-axis sets an upper limit on kx equal
to the Nyquist frequency
.Sampling on the x-axis sets an upper limit on kx equal
to the Nyquist frequency ![]() .Both frequency-domain methods and finite-difference methods
treat higher frequencies
as though they were folded back at the Nyquist frequency.
Thus the semicircle dispersion relation is
replicated above the Nyquist frequency,
as shown in Figure 19.
.Both frequency-domain methods and finite-difference methods
treat higher frequencies
as though they were folded back at the Nyquist frequency.
Thus the semicircle dispersion relation is
replicated above the Nyquist frequency,
as shown in Figure 19.
|
kxalias
Figure 19 The effective dispersion relation of the wave equation when the horizontal axis is sampled. Frequencies are given for typical zero-offset migration. | 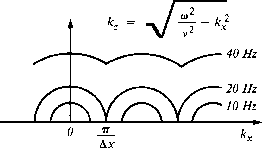 |
The problem of spatial aliasing begins when two circles touch each other,
as shown at 20 Hz in Figure 19.
This occurs when a half-wavelength v/2f equals
the spatial sample interval ![]() .The exploding-reflector model implies that the
velocity to use is half the rock velocity.
Thus the aliasing problem is avoided if
.The exploding-reflector model implies that the
velocity to use is half the rock velocity.
Thus the aliasing problem is avoided if
![]() .For a rock velocity equal to 2 km/sec, the safe frequencies
are listed in the table below:
.For a rock velocity equal to 2 km/sec, the safe frequencies
are listed in the table below:
| safe frequency | ||
| standard | 25m | <20Hz |
| reconnaissance | 50m | <10Hz |
| 3-D cross line | 100m | <5Hz |
Another view of the spatial aliasing problem is that steeply dipping waves
are suppressed by the geophone group.
(This disregards shot-space aliasing).
From this standpoint the limit
past which spatial aliasing begins should be thought
of in terms of angles at which energy is missing from the data.
Taking the ray angle to be 30![]() instead of 90
instead of 90![]() doubles
horizontal wavelengths.
Thus, for 30
doubles
horizontal wavelengths.
Thus, for 30![]() and a rock velocity of 2 km/sec,
to ensure safety from aliasing,
frequencies should be in the ranges listed below:
and a rock velocity of 2 km/sec,
to ensure safety from aliasing,
frequencies should be in the ranges listed below:
| safe frequency | ||
| standard | 25m | <40Hz |
| reconnaissance | 50m | <20Hz |
| 3-D cross line | 100m | <10Hz |
Because data usually has good signal above 40 Hz, wide-angle processing is often frustrated by spatial aliasing.
The problem of spatial aliasing usually overshadows the difference between
the 15![]() and the 90
and the 90![]() equations.
Aliased energy does not move between hyperbola flanks and the apex.
Aliased energy tends to stay in place.
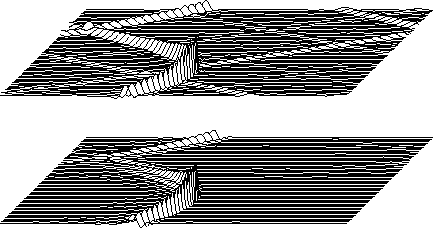
This is illustrated on Figure 20 which shows
a 90
equations.
Aliased energy does not move between hyperbola flanks and the apex.
Aliased energy tends to stay in place.
This is illustrated on Figure 20 which shows
a 90![]() hyperbola and a 15
hyperbola and a 15![]() hyperboloid
from a finite difference equation.
Overall, there is little difference.
Look at the amplitude of the hyperbolic arrival.
It is dropping off faster than predicted by spherical spreading and
the obliquity function.
This is because the dispersion curve semicircles overlap one another.
There can be no angles of propagation beyond
that which aliases x.
Since waves can't go so steeply, they don't.
The pulse doesn't spread properly.
hyperboloid
from a finite difference equation.
Overall, there is little difference.
Look at the amplitude of the hyperbolic arrival.
It is dropping off faster than predicted by spherical spreading and
the obliquity function.
This is because the dispersion curve semicircles overlap one another.
There can be no angles of propagation beyond
that which aliases x.
Since waves can't go so steeply, they don't.
The pulse doesn't spread properly.
 |