




Next: Extrapolation equations are not
Up: ANISOTROPY DISPERSION IN MIGRATION
Previous: Derivation of group velocity
Energy migration in (x,t)-space is analyzed in a fashion similar
to the way the group velocity was derived.
Take depth to be large in the integral
| ![\begin{displaymath}
\int \int \ e^{ i\,z\, [ k_z ( \omega , k_x ) \ -\ \omega \ t / z \ +\
k_x \ x / z ] } \ d \omega \ dk_x\end{displaymath}](img88.gif) |
(28) |
The result is that the energy goes to
| 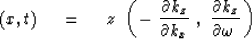 |
(29) |
This justifies our previous assertion
that (20) and (21) can be used to analyze
energy propagation errors.
Equation (29) was also used
to calculate the curve in Figure 9.
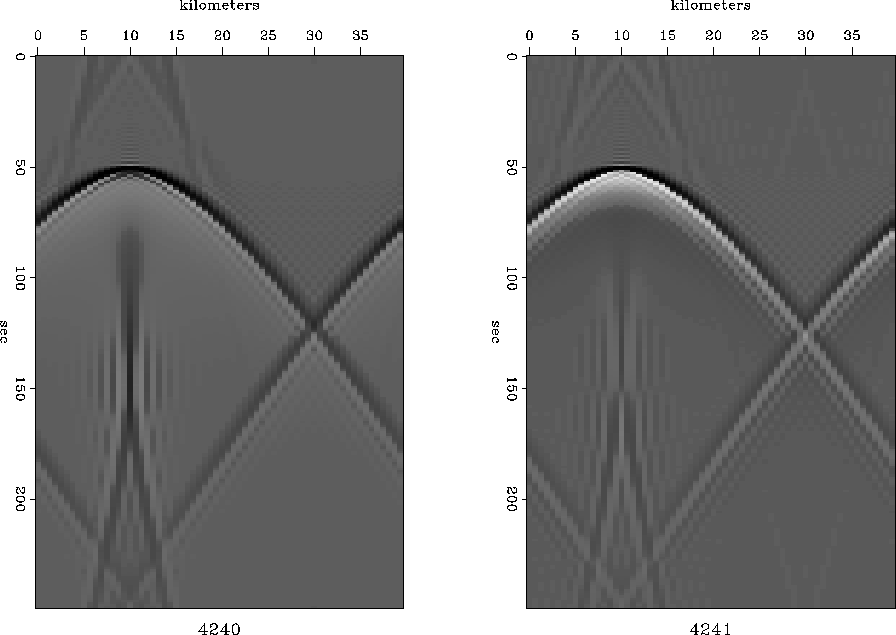
The validity of the stationary phase concept
is confirmed by Figure 16,
which was produced using inverse Fourier transformation.
aniso45
Figure 16
Impulse response of the 45 wave-extrapolation equation.
The arrival before t0 is a wraparound. wave-extrapolation equation.
The arrival before t0 is a wraparound.
|
|  |










Next: Extrapolation equations are not
Up: ANISOTROPY DISPERSION IN MIGRATION
Previous: Derivation of group velocity
Stanford Exploration Project
10/31/1997
