




Next: Derivation of energy migration
Up: ANISOTROPY DISPERSION IN MIGRATION
Previous: Analyzing errors of migration
An impulse function at the origin in (x,z)-space
is a superposition of Fourier components:
| 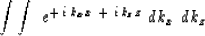 |
(22) |
Physics (and perhaps numerical analysis) leads to a dispersion relation
that is a functional relation
between 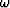 , kx, and kz,
say,
, kx, and kz,
say, 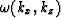 .
The most common example of such a dispersion relation
is the scalar wave
equation
.
The most common example of such a dispersion relation
is the scalar wave
equation 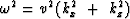 .The solution to the equation is
.The solution to the equation is
| 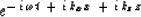 |
(23) |
Integrating (23) over (kx , kz ) produces a monochromatic
time function that at t = 0 is an impulse at (x,z) = (0,0).
This expression at some very large time t is
| ![\begin{displaymath}
\int \int \ e^{ -\,i\,t\, [ \omega (k_x , k_z ) \ -\ k_x
\ x / t \ -\ k_z \ z / t ] } \ dk_x \ dk_z\end{displaymath}](img85.gif) |
(24) |
At t very large, the integrand is a
very rapidly oscillating function
of unit magnitude.
Thus the integral will be nearly zero unless the quantity
in square brackets is found to be
nearly independent of kx and kz for some sizable area
in (kx , kz )-space.
Such a flat spot can be found in the same way that the maximum
or minimum of any two dimensional function is found,
by setting derivatives equal to zero.
This analytical approach is known as the stationary phase method.
It gives
| 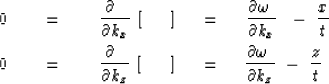 |
(25) |
| (26) |
So, in conclusion, at time t the disturbances will be located at
| 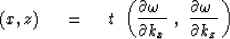 |
(27) |
which justifies the definition of group velocity.
Now let us see how the left side of
Figure 8 was calculated.
The 15 dispersion relation was solved for
dispersion relation was solved for 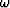 and
inserted into (27).
The resulting (x,z) turned out to be a function of
and
inserted into (27).
The resulting (x,z) turned out to be a function of 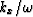 .Trying all possible values of
.Trying all possible values of 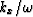 gave the curve.
gave the curve.





Next: Derivation of energy migration
Up: ANISOTROPY DISPERSION IN MIGRATION
Previous: Analyzing errors of migration
Stanford Exploration Project
10/31/1997
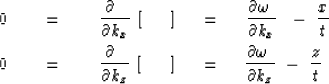
![]() dispersion relation was solved for
dispersion relation was solved for ![]() and
inserted into (27).
The resulting (x,z) turned out to be a function of
and
inserted into (27).
The resulting (x,z) turned out to be a function of ![]() .Trying all possible values of
.Trying all possible values of ![]() gave the curve.
gave the curve.