Conjugate Gradient Definition

The use of conjugate gradients helps to speed convergence by choosing a direction that is a linear combination of the past and current steepest descent vectors Luenberger (1984). Following Mora (1987), I use a conjugate gradient approach given by Polak and Ribiére (1969)

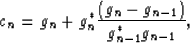$$c_n = g_n + g^{*}_n \frac{ \left( g_n - g_{n-1} \right)}{g^{*}_{n-1}g_{n-1} },$$ (10)

where c_n is the conjugate gradient update. Note that this is equivalent to the formulation in Mora (1987) where data and model space covariances are represented by identity operators. Equation 5 thus modifies to

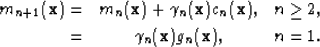$$\begin{eqnarray} m_{n+1} ({\bf x}) = & m_n ({\bf x}) + \gamma_n ({\bf x}) c_n ({... ... 2, \nonumber \ \; = & \gamma_n ({\bf x}) g_n ({\bf x}) , & n=1.\end{eqnarray}$$ (11)

The computation of conjugate gradient direction in equation 11 comes essentially at no cost because the previous gradient vector, g_n-1, easily can be stored in memory.