




Next: Example 2 - Polar
Up: Shragge: GRWE
Previous: Split-Step Fourier Approximation
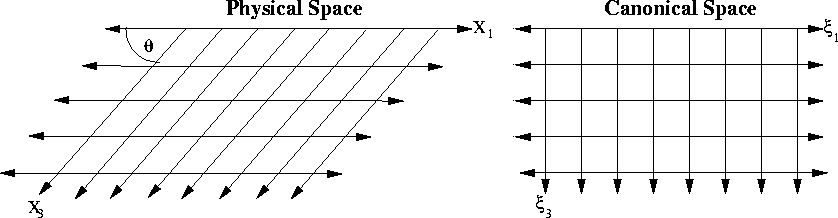
An instructive example is a coordinate system formed by a shearing
action on a Cartesian mesh (see figure ![[*]](http://sepwww.stanford.edu/data/media/public/sep/latex2html/cross_ref_motif.gif) ). A sheared
Cartesian coordinate system is defined by,
). A sheared
Cartesian coordinate system is defined by,
| ![\begin{displaymath}
\left[\begin{array}
{c}
x_1\ x_2\ x_3
\end{array}\rig...
...egin{array}
{c}
\xi_1\ \xi_2\ \xi_3\ \end{array}\right],\end{displaymath}](img46.gif) |
(21) |
where 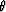 is the shear angle of the coordinate system
(
is the shear angle of the coordinate system
(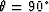 is Cartesian).
is Cartesian).
2Dexamp
Figure 1 2-D sheared Cartesian
coordinates. Left panel: Physical domain represented by sheared
Cartesian coordinates defined by 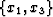 ; Right panel:
GRWE domain chosen to be the unit square ; Right panel:
GRWE domain chosen to be the unit square 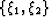 . . |
|  |

This system reduces to a more workable set of two equations,
| ![\begin{displaymath}
\left[\begin{array}
{c}
x_1\ x_3
\end{array}\right]
=...
... \left[\begin{array}
{c}
\xi_1\ \xi_3\ \end{array}\right],\end{displaymath}](img51.gif) |
(22) |
that has a metric tensor gij given by,
| ![\begin{displaymath}
\left[g_{ij}\right]
=
\left[\begin{array}
{cc}
\frac{\partia...
... \rm{cos}\, \theta \ \rm{cos}\,\theta & 1 \end{array}\right],\end{displaymath}](img52.gif) |
(23) |
with a determinant 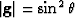 and an associated
metric tensor gij given by,
and an associated
metric tensor gij given by,
| ![\begin{displaymath}
\left[g^{ij}\right]
=
\frac{1}{\rm{sin}^2\,\theta}
\left[\be...
...- \rm{cos}\,\theta \ -\rm{cos}\,\theta & 1\end{array}\right].\end{displaymath}](img54.gif) |
(24) |
Note that because the tensor in equation 24 is
coordinate invariant, equation 10 simplifies to,
| 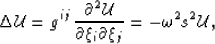 |
(25) |
and generates the following dispersion relation,
| 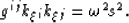 |
(26) |
Expanding out these terms leads to an expression for wavenumber 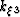 ,
,
| 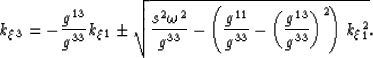 |
(27) |
Substituting the values of the associated metric tensor in
equation 24 into equation 27 yields,
| 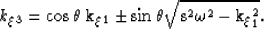 |
(28) |
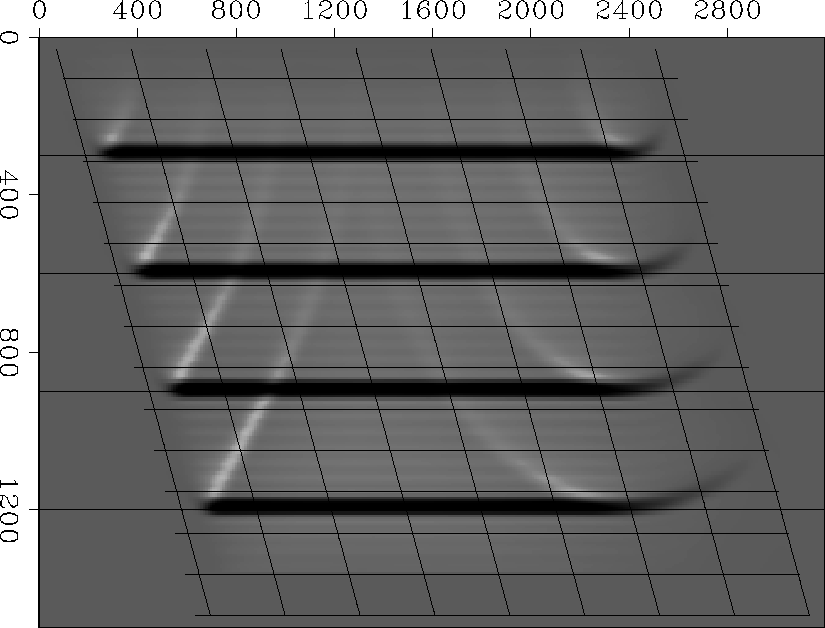
A numerical test using a Cartesian coordinate system sheared at
25 from vertical is shown in figure
from vertical is shown in figure ![[*]](http://sepwww.stanford.edu/data/media/public/sep/latex2html/cross_ref_motif.gif) .
The background velocity model is 1500 ms-1 and the zero-offset
data consist of 4 flat plane-waves t=0.2, 0.4, 0.6 and 0.8 s.
As expected, the zero-offset migration results image reflectors at
depths z=300, 600, 900, and 1200 m. Note that the propagation has
created boundary artifacts: those on the left are reflections due to a
truncated coordinate system while those on the right are hyperbolic
diffractions caused by truncated plane-waves.
.
The background velocity model is 1500 ms-1 and the zero-offset
data consist of 4 flat plane-waves t=0.2, 0.4, 0.6 and 0.8 s.
As expected, the zero-offset migration results image reflectors at
depths z=300, 600, 900, and 1200 m. Note that the propagation has
created boundary artifacts: those on the left are reflections due to a
truncated coordinate system while those on the right are hyperbolic
diffractions caused by truncated plane-waves.
Rays0
Figure 2 Sheared Cartesian coordinate
system test. Coordinate system shear angle and velocity are
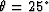 and 1500 ms-1, respectively. Zero-offset
data consist of 4 flat plane-wave impulses at t=0.2, 0.4, 0.6 and
0.8 s that are correctly imaged at depths z=300, 600, 900, and
1200 m. and 1500 ms-1, respectively. Zero-offset
data consist of 4 flat plane-wave impulses at t=0.2, 0.4, 0.6 and
0.8 s that are correctly imaged at depths z=300, 600, 900, and
1200 m.
|
|  |










Next: Example 2 - Polar
Up: Shragge: GRWE
Previous: Split-Step Fourier Approximation
Stanford Exploration Project
4/5/2006
![\begin{displaymath}
\left[\begin{array}
{c}
x_1\ x_2\ x_3
\end{array}\rig...
...egin{array}
{c}
\xi_1\ \xi_2\ \xi_3\ \end{array}\right],\end{displaymath}](img46.gif)
![[*]](http://sepwww.stanford.edu/data/media/public/sep/latex2html/cross_ref_motif.gif) ). A sheared
Cartesian coordinate system is defined by,
). A sheared
Cartesian coordinate system is defined by,
![\begin{displaymath}
\left[\begin{array}
{c}
x_1\ x_2\ x_3
\end{array}\rig...
...egin{array}
{c}
\xi_1\ \xi_2\ \xi_3\ \end{array}\right],\end{displaymath}](img46.gif)

![\begin{displaymath}
\left[g_{ij}\right]
=
\left[\begin{array}
{cc}
\frac{\partia...
... \rm{cos}\, \theta \ \rm{cos}\,\theta & 1 \end{array}\right],\end{displaymath}](img52.gif)
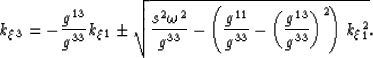
![]() from vertical is shown in figure
from vertical is shown in figure ![[*]](http://sepwww.stanford.edu/data/media/public/sep/latex2html/cross_ref_motif.gif) .
The background velocity model is 1500 ms-1 and the zero-offset
data consist of 4 flat plane-waves t=0.2, 0.4, 0.6 and 0.8 s.
As expected, the zero-offset migration results image reflectors at
depths z=300, 600, 900, and 1200 m. Note that the propagation has
created boundary artifacts: those on the left are reflections due to a
truncated coordinate system while those on the right are hyperbolic
diffractions caused by truncated plane-waves.
.
The background velocity model is 1500 ms-1 and the zero-offset
data consist of 4 flat plane-waves t=0.2, 0.4, 0.6 and 0.8 s.
As expected, the zero-offset migration results image reflectors at
depths z=300, 600, 900, and 1200 m. Note that the propagation has
created boundary artifacts: those on the left are reflections due to a
truncated coordinate system while those on the right are hyperbolic
diffractions caused by truncated plane-waves.
