Splitting and merging

As illustrated by Figure 3, the local-stationary algorithm splits the given nonstationary data set ${\bf d}$ into predefined stationary patches ${\bf d}_i$: 

$$\left[ \begin{array} {c} {\bf d}_1 \\ {\bf d}_2 \\ {\bf d}_3... ...f P}_1 \\ {\bf P}_2 \\ {\bf P}_3 \\ \end{array}\right] {\bf d}.$$ (1)

Each patch is then processed individually by a local stationary operator ${\bf F}_i: \Omega_{d_i} \rightarrow \Omega_{m_i}$:

$$\left[ \begin{array} {c} {\bf m}_1 \\ {\bf m}_2 \\ {\bf m}_3... ... {c} {\bf d}_1 \\ {\bf d}_2 \\ {\bf d}_3 \\ \end{array}\right].$$

Finally, an interpolation operator ${\bf Q} = [{\bf Q}_1, {\bf Q}_2, {\bf Q}_3]$ combines the processed patches ${\bf m}_i$ to a single output quilt ${\bf m}$: 

$${\bf m} = \left[ \begin{array} {ccc} {\bf Q}_1 & {\bf Q}_2... ... {c} {\bf m}_1 \\ {\bf m}_2 \\ {\bf m}_3 \\ \end{array}\right].$$ (2)

In summary, the patching algorithm is a compounding of windowing ${\bf P}^T = [{\bf P}_1, {\bf P}_2, {\bf P}_3]$, local imaging ${\bf F} = Diag({\bf F}_1, {\bf F}_2, {\bf F}_3)$, and merging ${\bf Q}^T = [{\bf Q}_1, {\bf Q}_2, {\bf Q}_3]$:

$${\bf m} = {\bf Q}^T {\bf F} {\bf P} {\bf d}.$$

 

quiltPatch
Figure 3 Patching scheme of local-stationary data. The algorithm extracts data patches from the data quilt. It images each patch by the corresponding stationary operator. Finally, it merges the individual patches to a single output quilt. The isolation of the individual patches makes this algorithm suitable for nonlinear, data-dependent operators.

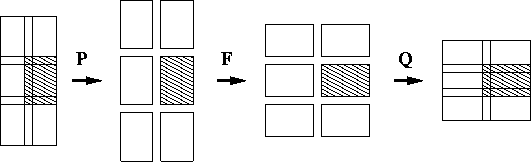This algorithm applies each stationary operator exclusively to its appropriate patch. The individual patches can conveniently be used to estimate the desired operator, should it be dependent on its stationary input data. If, for example, the operators ${\bf F}_i$ are to deconvolve an unknown local blur, the isolated stationary patches conveniently permit the estimation of the optimal coefficients for the local deconvolution filter. However, this algorithm has to manipulate the space information of its various patches and quilts carefully: a task, the vector spaces of my Java software library Jest excel at.

If the operator ${\bf F}$ has identical domain and range, the initial windowing step (1) and the final merging step (2) could be implemented by adjoint operators: a column of truncation operators ${\bf P}_i$ and a row of zero padding operators ${\bf Q}_i = {\bf P}^T_i$. In general, the internal stationary operators ${\bf F}_i$, however, causes the range and domain of the splitting and interpolation operation to differ. Furthermore, a row of zero-padding operators amounts to stacking of the individual patches into the output quilt. To avoid visible boundaries at the edges of the patches, we usually prefer more sophisticated interpolation schemes.