




Next: Linearization
Up: Alkhalifah and Fomel: Anisotropy
Previous: Introduction
In the case of zero-offset reflection, the ray travel distance,
l, from the source to the reflection point is related to the
two-way zero-offset time, t, by the simple equation
where vg is the half of the group velocity, best expressed in
terms of its components, as follows:
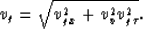
Here vgx denotes the horizontal component of group velocity,
vv is the vertical P-wave velocity, and 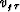 is the
vv-normalized vertical component of the group velocity. Under the
assumption of zero shear-wave velocity in VTI media, these components
have the following analytic expressions:
is the
vv-normalized vertical component of the group velocity. Under the
assumption of zero shear-wave velocity in VTI media, these components
have the following analytic expressions:
| 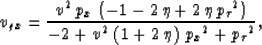 |
(4) |
and
| 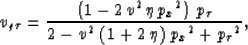 |
(5) |
where px is the horizontal component of slowness, and 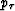 is the normalized (again by the vertical P-wave velocity vv)
vertical component of slowness. The two components of the slowness
vector are related by the following eikonal-type equation
Alkhalifah (1997):
is the normalized (again by the vertical P-wave velocity vv)
vertical component of slowness. The two components of the slowness
vector are related by the following eikonal-type equation
Alkhalifah (1997):
| 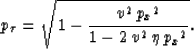 |
(6) |
Equation (6) corresponds to a normalized version of the
dispersion relation in VTI media.
If we consider v and  as imaging parameters (migration
velocity and migration anisotropy coefficient), the ray length l can
be taken as an imaging invariant. This implies that the partial
derivatives of l with respect to the imaging parameters are zero.
Therefore,
as imaging parameters (migration
velocity and migration anisotropy coefficient), the ray length l can
be taken as an imaging invariant. This implies that the partial
derivatives of l with respect to the imaging parameters are zero.
Therefore,
| 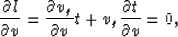 |
(7) |
and
| 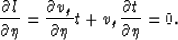 |
(8) |
Applying the simple chain rule to equations (7) and
(8), we obtain
| 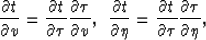 |
(9) |
where 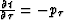 , and the two-way vertical traveltime is
given by
, and the two-way vertical traveltime is
given by
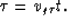
Combining equations (7-9) eliminates the two-way
zero-offset time t, which leads to the equations
| 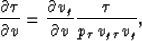 |
(10) |
and
| 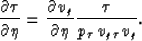 |
(11) |
After some tedious algebraic manipulation, we can transform
equations (5) and (6) to the general form
| 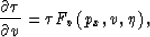 |
(12) |
and
| 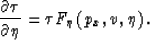 |
(13) |
Since the residual migration is applied to migrated data, with the
time axis given by  and the reflection slope given by
and the reflection slope given by
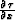 , instead of t and px,
respectively, we need to eliminate px from
equations (12) and (13). This task can be
achieved with the help of the following explicit relation, derived
in Appendix A,
, instead of t and px,
respectively, we need to eliminate px from
equations (12) and (13). This task can be
achieved with the help of the following explicit relation, derived
in Appendix A,
| 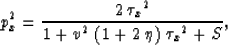 |
(14) |
where 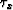 =
=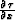 , and
, and
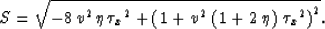
Inserting equation (14) into equations (12)
and (13) yields exact, yet complicated equations,
describing the continuation process for v and  . In
summary, these equations have the form
. In
summary, these equations have the form
| 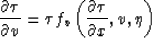 |
(15) |
and
| 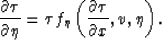 |
(16) |
Equations of the form (15) and (16) contain all
the necessary information about the kinematic laws of anisotropy
continuation in the domain of zero-offset migration.





Next: Linearization
Up: Alkhalifah and Fomel: Anisotropy
Previous: Introduction
Stanford Exploration Project
11/11/1997
![]()
![]() as imaging parameters (migration
velocity and migration anisotropy coefficient), the ray length l can
be taken as an imaging invariant. This implies that the partial
derivatives of l with respect to the imaging parameters are zero.
Therefore,
as imaging parameters (migration
velocity and migration anisotropy coefficient), the ray length l can
be taken as an imaging invariant. This implies that the partial
derivatives of l with respect to the imaging parameters are zero.
Therefore,
![]()
![]() and the reflection slope given by
and the reflection slope given by
![]() , instead of t and px,
respectively, we need to eliminate px from
equations (12) and (13). This task can be
achieved with the help of the following explicit relation, derived
in Appendix A,
, instead of t and px,
respectively, we need to eliminate px from
equations (12) and (13). This task can be
achieved with the help of the following explicit relation, derived
in Appendix A,
![]()
![]() . In
summary, these equations have the form
. In
summary, these equations have the form