




Next: Better stationary-phase approximations
Up: Analytical Approximations of the
Previous: Isotropic homogeneous media
The time-processing operators in VTI media, as mentioned earlier, depend primarily on two parameters,
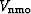 and
and  . This dependency becomes exact when the shear wave velocity (VS0) is
set to zero (Alkhalifah, 1997c). Setting VS0=0, although not practical for TI media, yields
remarkably accurate kinematic representations. Errors due to this approximation,
for practical VTI models,
are kinematically, in a worse-case scenario, less than 0.5 percent, which is far
within the limits of seismic accuracy.
This acoustic approximation yields simplified equations, including a simplified dispersion
relation. Because the vertical P-wave velocity does not have any significance in time-related
processing in VTI media (Alkhalifah and Tsvankin, 1995), I will refer to
. This dependency becomes exact when the shear wave velocity (VS0) is
set to zero (Alkhalifah, 1997c). Setting VS0=0, although not practical for TI media, yields
remarkably accurate kinematic representations. Errors due to this approximation,
for practical VTI models,
are kinematically, in a worse-case scenario, less than 0.5 percent, which is far
within the limits of seismic accuracy.
This acoustic approximation yields simplified equations, including a simplified dispersion
relation. Because the vertical P-wave velocity does not have any significance in time-related
processing in VTI media (Alkhalifah and Tsvankin, 1995), I will refer to 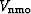 as the velocity and
denote it by the symbol v to simplify comparisons with isotropic media.
The zero-offset time-migration dispersion relation for VTI media, when VS0=0, is given by
as the velocity and
denote it by the symbol v to simplify comparisons with isotropic media.
The zero-offset time-migration dispersion relation for VTI media, when VS0=0, is given by
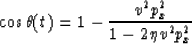
(Alkhalifah, 1997c). Based on this relation, the normalized DSR equation, for VTI media, has the form
| 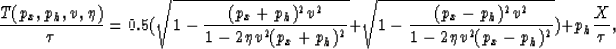 |
(33) |
Clearly, for  =0, the above equations reduce to there isotropic counterparts.
The stationary point (or points) satisfy the following relation
=0, the above equations reduce to there isotropic counterparts.
The stationary point (or points) satisfy the following relation
| 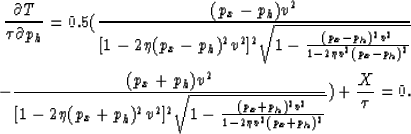 |
|
| (34) |
ph1eta2m
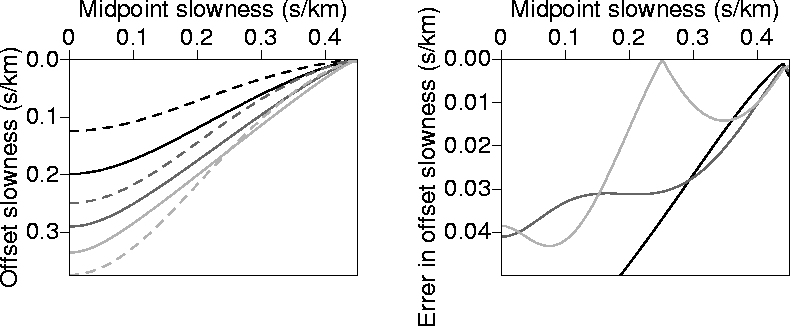
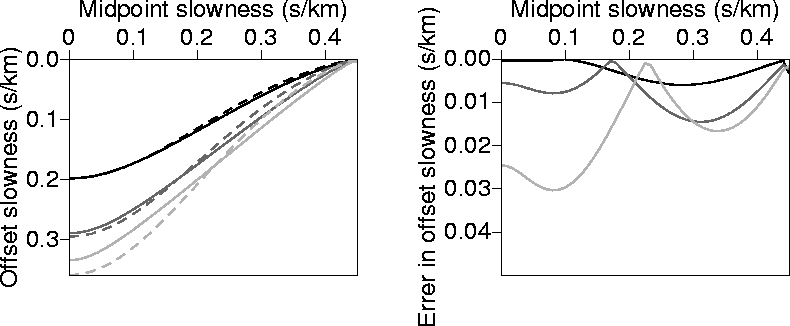
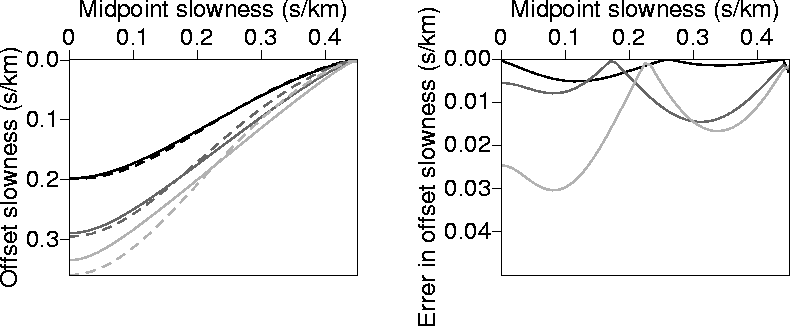
Figure 20 Left: Values of ph as a function px calculated numerically
(solid curves), and calculated analytically (dashed curves) using equation (B-1). Right: The absolute difference
between the two curves on the right. The medium is homogeneous and transversely isotropic with v=2.0 km/s
and  =0.2..
The black curve corresponds to
=0.2..
The black curve corresponds to 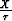 =1.0 (km/s), the dark-gray curve corresponds to
=1.0 (km/s), the dark-gray curve corresponds to
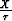 =2.0 (km/s), and the light gray curve corresponds to
=2.0 (km/s), and the light gray curve corresponds to 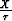 =3.0 (km/s).
=3.0 (km/s).

Following the same approach used in the previous sections for isotropic media, we set px=0, and
as a result, equation (B-10) reduces to
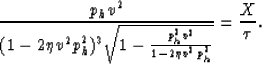
Squaring both sides and expanding in ph, we get
![\begin{displaymath}
8 \eta^3 X^2 (1+2 \eta) y^4 - 4 \eta^2 X^2 (3+8 \eta) y^3 + ...
...X^2 (1+4 \eta) y^2 -
[X^2 (1+8 \eta)+ \tau^2 v^2] y + X^2 = 0, \end{displaymath}](img100.gif)
where y=ph2 v2. This is a quartic equation in y, which, although,it has analytical solutions,
is best solved numerically.
Considering either  or y (
or y (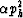 ), or both, to be small, we can drop terms of y
beyond the quadratic (perturbation theory; Bender and Orszag, 1978) , and as a result, the quartic equation reduces to
), or both, to be small, we can drop terms of y
beyond the quadratic (perturbation theory; Bender and Orszag, 1978) , and as a result, the quartic equation reduces to
a y2 +b y +c =0,
where
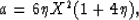
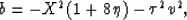
and
Because  can be small, as small as zero for isotropic media,
I prefer to use the following form of solution of the quadratic equation:
can be small, as small as zero for isotropic media,
I prefer to use the following form of solution of the quadratic equation:
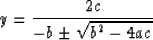
(Press et al., 1988).
Thus,
| 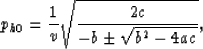 |
(36) |
where the positive-sign root is used. The negative-sign root results in an imaginary
ph solution which is clearly not the solution we are looking for. Another, yet better,
approximation is described in Appendix C using perturbation series as well as
Shanks transformation. For  =0 (isotropic media),
a=0, and this equation reduces to equation (B-3), which is
its isotropic counterpart. This is amazing considering we have dropped some terms in solving
the quartic equation.
Equation (B-11)
is not the exact solution for horizontal reflectors in VTI media. However, as we will see bellow, it is
a good approximation; better than similar approximations based on Taylors series
expansion of traveltimes around the zero-offset point.
Also, to insure we do not get imaginary roots for ph, b2-4ac must be greater or equal
zero. This results in the following condition that must be satisfied:
=0 (isotropic media),
a=0, and this equation reduces to equation (B-3), which is
its isotropic counterpart. This is amazing considering we have dropped some terms in solving
the quartic equation.
Equation (B-11)
is not the exact solution for horizontal reflectors in VTI media. However, as we will see bellow, it is
a good approximation; better than similar approximations based on Taylors series
expansion of traveltimes around the zero-offset point.
Also, to insure we do not get imaginary roots for ph, b2-4ac must be greater or equal
zero. This results in the following condition that must be satisfied:
![\begin{displaymath}
\tau^2 \gt [2 \sqrt{6 \eta (1+4 \eta)} - (1+8 \eta)] \frac{X^2}{v^2},\end{displaymath}](img106.gif)
which corresponds to large offset-to-depth ratio. For practical values of  (<0.3), this condition
is far within the typical mute zone. For example, if
v=2 km/s,
(<0.3), this condition
is far within the typical mute zone. For example, if
v=2 km/s, 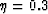 , and X=3 km,
, and X=3 km,  =1.14 s.
=1.14 s.
Expanding equation (B-10) using Taylors series,
around ph=0 (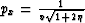 ),
and ignoring terms beyond the linear, yields
),
and ignoring terms beyond the linear, yields
| 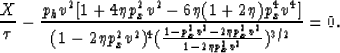 |
(37) |
As a result, the stationary point is given by
| ![\begin{displaymath}
p_h = \frac{\frac{X}{\tau}}{v^2} \frac{(1-2 \eta p_x^2 v^2)^...
...v^2})^{3/2}}{[1+4 \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]}.\end{displaymath}](img110.gif) |
(38) |
Again, I insert equation (B-11) in place of 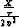 , and obtain
, and obtain
| ![\begin{displaymath}
p_h = \frac{1}{v} \sqrt{\frac{2 c}{-b \pm \sqrt{b^2-4ac}}} \...
...v^2})^{3/2}}{[1+4 \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]}.\end{displaymath}](img112.gif) |
(39) |
where a, b, and c are given by equation (B-11).
Equation (B-15) is exact for 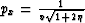 (ph=0).
However, unlike the isotropic
medium case, equation (B-15) is
an approximation at px=0. [Recall that we dropped terms beyond
the quadratic in equation (B-13).] Despite the approximation used at px=0,
I will refer to this equation as the 2-point solution for VTI media.
ph2eta2m
(ph=0).
However, unlike the isotropic
medium case, equation (B-15) is
an approximation at px=0. [Recall that we dropped terms beyond
the quadratic in equation (B-13).] Despite the approximation used at px=0,
I will refer to this equation as the 2-point solution for VTI media.
ph2eta2m
Figure 21 Same as in Figure B-1, but with the analytical solution evaluated
using the 2-point fitting of equation (B-15).

Figure B-5 shows ph given by equation (B-15)
and compares it with the accurate result
calculated numerically from equation (B-10) for three sets of 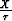 .
Despite the large non-hyperbolic moveout associated with horizontal events in
such VTI media (Alkhalifah, 1997b), the approximation at px=0, which corresponds to a horizontal
event, is rather good. Combine this with the fact that the phase [equation (B-9)]
changes slowly as a function of (or rather insensitive to) ph around the exact solution, the
result is a good approximation of the phase for all px (slopes).
.
Despite the large non-hyperbolic moveout associated with horizontal events in
such VTI media (Alkhalifah, 1997b), the approximation at px=0, which corresponds to a horizontal
event, is rather good. Combine this with the fact that the phase [equation (B-9)]
changes slowly as a function of (or rather insensitive to) ph around the exact solution, the
result is a good approximation of the phase for all px (slopes).
The accuracy of equation (B-15) can be further enhanced, as in the isotropic case,
by fitting it to the exact
solution for px=ph; the angular correspondence of this equality depends
on the offset-to-depth ratio. Following the same steps used to obtain the ph for px=0, including
dropping terms beyond the quadratic in a similar quartic equation to that of equation (B-13),
the stationary point is given by
| 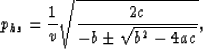 |
(40) |
where
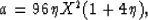
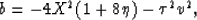
and
c=X2.
Equatio (B-16)n has a stricter condition for its validity (that is avoiding imaginary roots) than that
of equation (B-11). Specifically,
![\begin{displaymath}
\tau^2 \gt 4 [2 \sqrt{6 \eta (1+4 \eta)} - (1+8 \eta)] \frac{X^2}{v^2},\end{displaymath}](img116.gif)
which correspond to double the time for the horizontal reflector solution fitting. For
v=2 km/s, 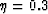 , and X=3 km,
, and X=3 km,  =2.28 s.
=2.28 s.
Again, inserting equation (B-16) into equation (B-15) requires solving two equations and,
similar to the case of isotropic media, the solution is given by
| ![\begin{displaymath}
p_h = p_{h0} \frac{(1-2 \eta p_x^2 v^2)^4
(\frac{1-p_x^2 v^...
... \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]} [a(p_{h0})p_x+b],\end{displaymath}](img117.gif) |
(41) |
where setting px=0 gives b=1 and setting px=phs results in
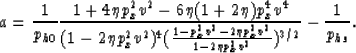
ph3eta2m
Figure 22 Same as in Figure B-1, but with the analytical solution evaluated
using the 3-point fitting of equation (B-17).

Figure B-6 shows the numerically-driven curves (solid ones) along with the analytical
curves
calculated using the 3-point fitting of equation B-17. The 3-point equation
provides the best estimation to the exact solution for 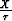 .
.





Next: Better stationary-phase approximations
Up: Analytical Approximations of the
Previous: Isotropic homogeneous media
Stanford Exploration Project
11/11/1997
![]() and
and ![]() . This dependency becomes exact when the shear wave velocity (VS0) is
set to zero (Alkhalifah, 1997c). Setting VS0=0, although not practical for TI media, yields
remarkably accurate kinematic representations. Errors due to this approximation,
for practical VTI models,
are kinematically, in a worse-case scenario, less than 0.5 percent, which is far
within the limits of seismic accuracy.
This acoustic approximation yields simplified equations, including a simplified dispersion
relation. Because the vertical P-wave velocity does not have any significance in time-related
processing in VTI media (Alkhalifah and Tsvankin, 1995), I will refer to
. This dependency becomes exact when the shear wave velocity (VS0) is
set to zero (Alkhalifah, 1997c). Setting VS0=0, although not practical for TI media, yields
remarkably accurate kinematic representations. Errors due to this approximation,
for practical VTI models,
are kinematically, in a worse-case scenario, less than 0.5 percent, which is far
within the limits of seismic accuracy.
This acoustic approximation yields simplified equations, including a simplified dispersion
relation. Because the vertical P-wave velocity does not have any significance in time-related
processing in VTI media (Alkhalifah and Tsvankin, 1995), I will refer to ![]() as the velocity and
denote it by the symbol v to simplify comparisons with isotropic media.
The zero-offset time-migration dispersion relation for VTI media, when VS0=0, is given by
as the velocity and
denote it by the symbol v to simplify comparisons with isotropic media.
The zero-offset time-migration dispersion relation for VTI media, when VS0=0, is given by
![]()
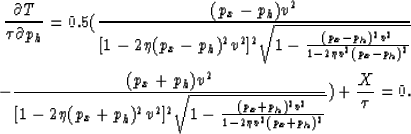
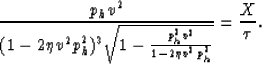
![]()
![]()
![]()
![]()
![]()
![]() ),
and ignoring terms beyond the linear, yields
),
and ignoring terms beyond the linear, yields
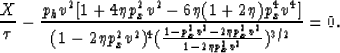
![\begin{displaymath}
p_h = \frac{\frac{X}{\tau}}{v^2} \frac{(1-2 \eta p_x^2 v^2)^...
...v^2})^{3/2}}{[1+4 \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]}.\end{displaymath}](img110.gif)
![\begin{displaymath}
p_h = \frac{1}{v} \sqrt{\frac{2 c}{-b \pm \sqrt{b^2-4ac}}} \...
...v^2})^{3/2}}{[1+4 \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]}.\end{displaymath}](img112.gif)
![]() .
Despite the large non-hyperbolic moveout associated with horizontal events in
such VTI media (Alkhalifah, 1997b), the approximation at px=0, which corresponds to a horizontal
event, is rather good. Combine this with the fact that the phase [equation (B-9)]
changes slowly as a function of (or rather insensitive to) ph around the exact solution, the
result is a good approximation of the phase for all px (slopes).
.
Despite the large non-hyperbolic moveout associated with horizontal events in
such VTI media (Alkhalifah, 1997b), the approximation at px=0, which corresponds to a horizontal
event, is rather good. Combine this with the fact that the phase [equation (B-9)]
changes slowly as a function of (or rather insensitive to) ph around the exact solution, the
result is a good approximation of the phase for all px (slopes).
![]()
![]()
![]()
![\begin{displaymath}
p_h = p_{h0} \frac{(1-2 \eta p_x^2 v^2)^4
(\frac{1-p_x^2 v^...
... \eta p_x^2 v^2-6 \eta (1+2 \eta) p_x^4 v^4]} [a(p_{h0})p_x+b],\end{displaymath}](img117.gif)
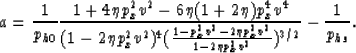
![]() .
.