Next: DEPTH MIGRATION OPERATOR UPDATE
Up: SCANNING HOMOTHETIC PARAMETER
Previous: Homothetic scaling of travel-times
To illustrate the homothetic scaling approach we
built a synthetic model (Figures 1 and 2),
and downward continued to the reflector.
If we start with an initial constant velocity model equal to the background
velocity
we see good
coherency at zero time at CMP locations far
away from the anomaly (Figure 3). For
CMP's closer to the
anomaly, focusing deteriorates and deviates from zero time.
layer.gauss
Figure 1 Input velocity model. Gaussian
anomaly at 4 km/s in an otherwise homogeneous half-space (3km/s).
|
|  |





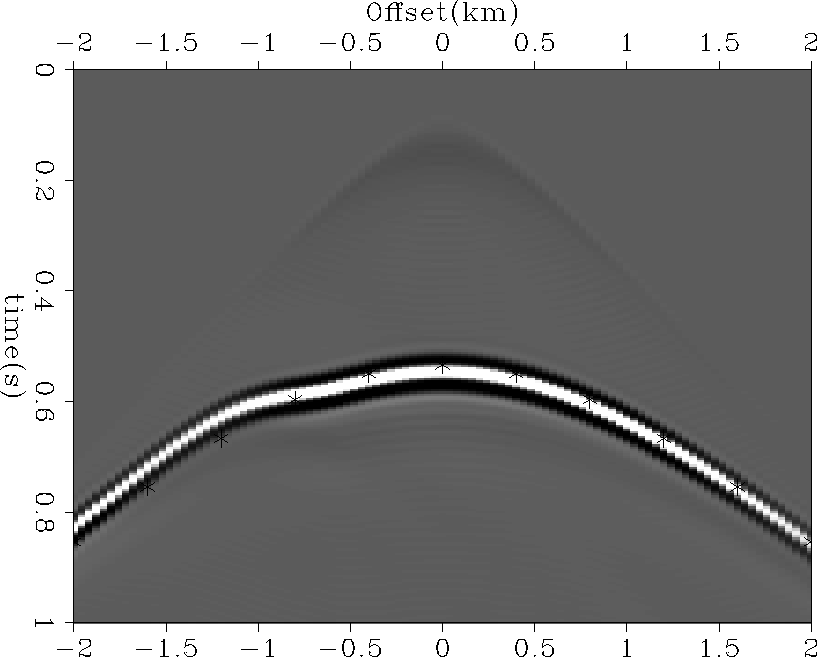
layer.shot
Figure 2 A sample shot gather
illustrating
the non-hyperbolic move-out (hyperbolic move-out indicated by `*')
caused by the velocity anomaly.
|
|  |




 layer.gama.1
layer.gama.1
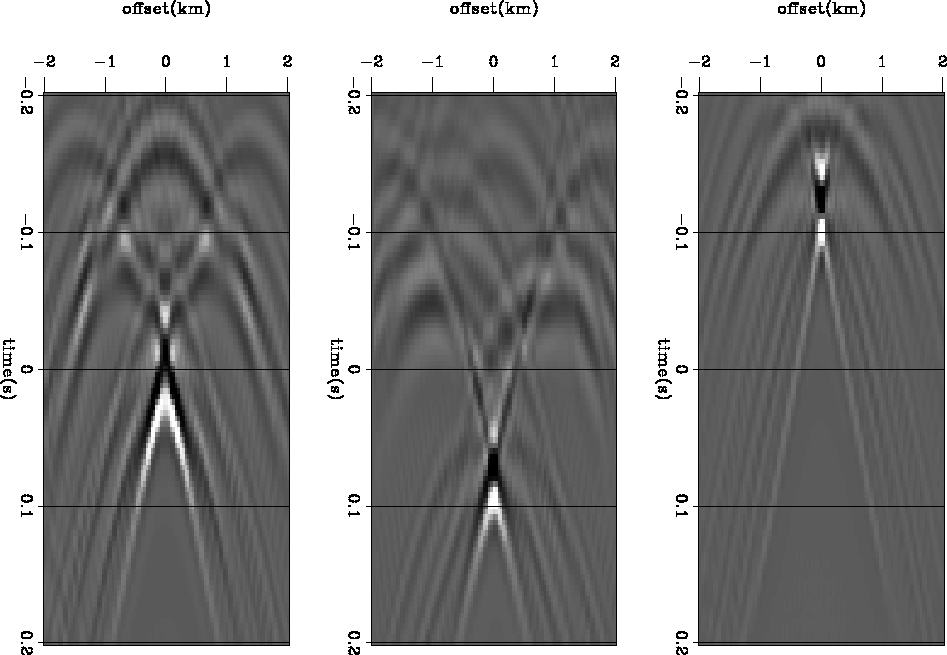
Figure 3 Result of downward
continuing at three different locations. The left panel is
far away from anomaly(CMP 8); the
center, at the edge of the anomaly(CMP 7);
and the right directly above anomaly(CMP 6).





We then found which scaled version of the travel-time
field best focused the data at various CMP locations.
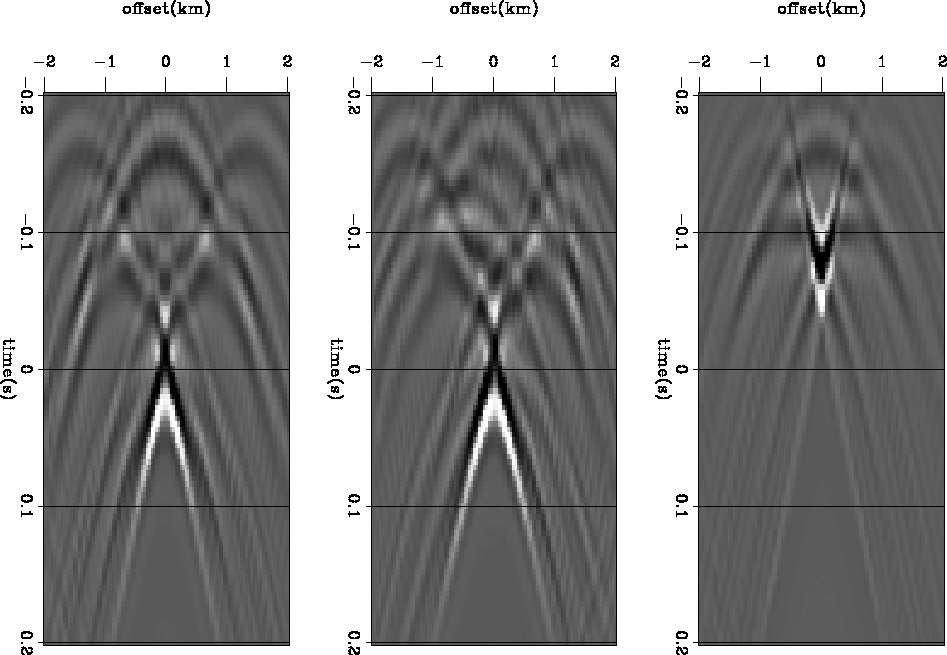
Figure 4
shows the optimal focusing result for the same three
CMP's as Figure 3.
As expected, away from the anomaly the best focusing occurs at zero time
when 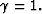 At the edge of the anomaly,
best focusing is achieved at positive time, with
At the edge of the anomaly,
best focusing is achieved at positive time, with 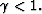 (outer offset
ray-paths pass through the anomaly, decreasing curvature, indicating a
faster velocity). While directly above the anomaly we see maximum focusing
at negative time, at
(outer offset
ray-paths pass through the anomaly, decreasing curvature, indicating a
faster velocity). While directly above the anomaly we see maximum focusing
at negative time, at 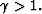 (inner offsets faster, more curvature,
indicating lower velocity and increased travel-times).
(inner offsets faster, more curvature,
indicating lower velocity and increased travel-times).
layer.gama.best
Figure 4 The best focusing 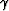 .The left, CMP 8,
.The left, CMP 8, 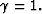 ;center, CMP 7,
;center, CMP 7, 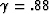 ; and right, directly above, CMP 6
; and right, directly above, CMP 6
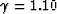 .
.










Next: DEPTH MIGRATION OPERATOR UPDATE
Up: SCANNING HOMOTHETIC PARAMETER
Previous: Homothetic scaling of travel-times
Stanford Exploration Project
11/11/1997



![]() At the edge of the anomaly,
best focusing is achieved at positive time, with
At the edge of the anomaly,
best focusing is achieved at positive time, with ![]() (outer offset
ray-paths pass through the anomaly, decreasing curvature, indicating a
faster velocity). While directly above the anomaly we see maximum focusing
at negative time, at
(outer offset
ray-paths pass through the anomaly, decreasing curvature, indicating a
faster velocity). While directly above the anomaly we see maximum focusing
at negative time, at ![]() (inner offsets faster, more curvature,
indicating lower velocity and increased travel-times).
(inner offsets faster, more curvature,
indicating lower velocity and increased travel-times).