![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
share a common polynomial form:
)
share a common polynomial form:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is enough for doing NMO and
assuming elliptical anisotropy accomplishes nothing more
than making explicit the depth ambiguity that was always there.
To add another velocity parameter to this isotropic (really
elliptically anisotropic) case, we need to add some sort of an
anelliptic parameter.
) is enough for doing NMO and
assuming elliptical anisotropy accomplishes nothing more
than making explicit the depth ambiguity that was always there.
To add another velocity parameter to this isotropic (really
elliptically anisotropic) case, we need to add some sort of an
anelliptic parameter.
Note that
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
share a common polynomial form:
)
share a common polynomial form:
| |
(9) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
by generalizing it to
)
by generalizing it to
| |
(10) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) reverts to the original elliptic form in
equation (
) reverts to the original elliptic form in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for all propagation directions.
) for all propagation directions.
Why this particular generalization?
This anelliptic form needs only one more parameter
beyond elliptical anisotropy (or isotropy for the surface survey case),
retains the properties that make elliptical anisotropy so convenient
(in approximation),
and makes a good approximation to exact transverse isotropy,
especially in the phase-slowness domain. (See Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .)
.)
Following this template,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) (the ray equation) becomes
) (the ray equation) becomes
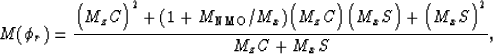 |
(11) |
We can similarly extend equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
(the dispersion relation) to
)
(the dispersion relation) to
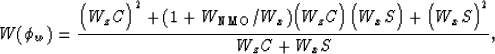 |
(12) |
Note the symmetry between
equations ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ;
as for elliptical anisotropy, converting from the representation in
one domain to the other is as simple as replacing each of the velocity
parameters with its reciprocal.
;
as for elliptical anisotropy, converting from the representation in
one domain to the other is as simple as replacing each of the velocity
parameters with its reciprocal.