Consistency

Although replacing each of the velocity parameters with its reciprocal is certainly convenient, the resulting pair of equations are unfortunately inconsistent: equation () implies a ray surface which does not satisfy equation (), and vice versa. This is not a problem in practice. We don't require exact consistency because these equations are only meant as approximations anyway. The original elliptical forms, equations () and (), are exactly consistent everywhere. Because equations () and () approximate the original elliptical equations paraxially around the z axis, our two anelliptic equations must also be approximately consistent paraxially around the z axis. Similarly, for propagation along the x axis the two new equations are each governed by the true horizontal velocity V_x. As a result they must be exactly consistent on the x axis as well and approximately consistent nearby.

Figure  shows the approximations in the group-velocity and phase-slowness domains for the qP surface of Greenhorn Shale (Jones and Wang, 1981), a transversely isotropic medium. As shown by the four plots, the approximations are reasonably consistent even away from the axial ``control points'' for the qP surface, despite the strongly non-elliptic anisotropy. (If the first anelliptic approximation in the two domains of interest were perfectly consistent with each other, the thick dashed line would follow the same trajectory relative to the thin continuous line in both columns. 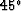As it is, at $45^\circ$ the approximation in the group domain underestimates the group velocity by 1.7% and the approximation in the phase domain overestimates the group velocity by .6%.) The three axial constraints seem to be enough to tie the two approximations to the underlying TI medium, and thus to each other.

The fit is not so good for the corresponding qSV surface, shown in Figure . This is not surprising as there is no way a single-valued ray equation can track a triplication. The approximation can still be used in the phase-slowness domain in such cases, but there is no hope that the phase- and group-domain approximations can be very consistent if the approximation in either domain is anywhere concave. Mathematically, for there to be no concavity in either domain the ``F'' factor in equation () (or F_z and F_x factors in equation ()) should satisfy the inequality

3/7 < F < 7/3 .