




Next: THE FIRST ANELLIPTIC APPROXIMATION
Up: Dellinger, Muir, & Karrenbach:
Previous: Introduction
Waves propagating in a homogeneous medium can be described and extrapolated
in either the time-space ``group'' or frequency-wavenumber ``phase'' domains.
In the standard scalar isotropic case life is simple;
there is one soundspeed characteristic
of the medium, and it is the same whether we are talking about
rays (group velocity) or plane waves (phase velocity).
The scalar isotropic ray (or group-velocity) equation in polar coordinates
is just
| 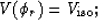 |
(1) |
the corresponding dispersion relation (phase-velocity equation)
is
| 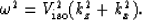 |
(2) |
With anisotropy the propagation velocity depends on the propagation direction,
and the group and phase velocities and directions are no longer the same.
Convenient closed-form ``group'' and ``phase'' equations like
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are usually
not simultaneously available.
Even worse,
the number of parameters required to describe the medium can
be intractably large.
) are usually
not simultaneously available.
Even worse,
the number of parameters required to describe the medium can
be intractably large.
Scalar elliptical anisotropy does not suffer from these difficulties.
There are only two velocities, horizontal and vertical.
It is true that the ray equation for scalar elliptical anisotropy
appears a bit complicated at first glance:
| 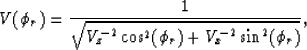 |
(3) |
where 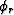 is the group-propagation (ray) direction
(with
is the group-propagation (ray) direction
(with 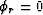 being vertical).
If we re-express equation (
being vertical).
If we re-express equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in terms of
slowness squared M = 1/V2, however,
it simplifies considerably:
) in terms of
slowness squared M = 1/V2, however,
it simplifies considerably:
| 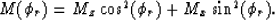 |
(4) |
The dispersion relation for elliptical anisotropy is similarly simple:
| 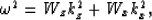 |
(5) |
where
Wz is the vertical velocity squared
and
Wx is the horizontal velocity squared.
Another form of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) displays the fundamental
nature of elliptical anisotropy more clearly.
If you divide equation (
) displays the fundamental
nature of elliptical anisotropy more clearly.
If you divide equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) through by
) through by
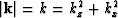 , you get
, you get
| 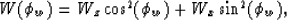 |
(6) |
where 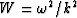 is phase-velocity squared and
is phase-velocity squared and
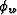 is the wave-propagation (phase) direction,
with
is the wave-propagation (phase) direction,
with 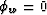 being vertical.
The identity of form between
equations (
being vertical.
The identity of form between
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is not accidental.
An ellipse is merely a stretched circle, and
elliptical anisotropy is merely stretched isotropy.
The Fourier similarity theorem
tells us that a ``stretch'' (linear transformation)
in the (x,z) domain corresponds to
an ``inverse stretch'' (another linear transformation)
in the (kx, kz) domain.
Equations (
) is not accidental.
An ellipse is merely a stretched circle, and
elliptical anisotropy is merely stretched isotropy.
The Fourier similarity theorem
tells us that a ``stretch'' (linear transformation)
in the (x,z) domain corresponds to
an ``inverse stretch'' (another linear transformation)
in the (kx, kz) domain.
Equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
look the same because they are both equations for stretched circles,
i.e., ellipses.
)
look the same because they are both equations for stretched circles,
i.e., ellipses.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how elliptical anisotropy can be used as
a first-order paraxial approximation in both the group and phase domains.
Although the group-velocity and phase-slowness representations
of this transversely isotropic medium look very different,
the first-order paraxial approximation is elliptical in both domains.
(The TI medium is Greenhorn Shale from Jones and Wang (1981).)
shows how elliptical anisotropy can be used as
a first-order paraxial approximation in both the group and phase domains.
Although the group-velocity and phase-slowness representations
of this transversely isotropic medium look very different,
the first-order paraxial approximation is elliptical in both domains.
(The TI medium is Greenhorn Shale from Jones and Wang (1981).)
This paraxial ellipse is also of considerable practical importance.
The familiar isotropic moveout equation is
| 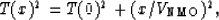 |
(7) |
where T(x) is the traveltime at offset x,
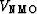 is the moveout velocity,
h is the vertical layer thickness,
and Vz is the vertical velocity.
(This is one-way traveltime.)
In the isotropic case we only have one velocity, and set
is the moveout velocity,
h is the vertical layer thickness,
and Vz is the vertical velocity.
(This is one-way traveltime.)
In the isotropic case we only have one velocity, and set
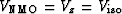 .Converting from isotropy to elliptical anisotropy with a vertical axis
is as simple as replacing z with a new stretched coordinate
.Converting from isotropy to elliptical anisotropy with a vertical axis
is as simple as replacing z with a new stretched coordinate
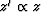 . Because the z coordinate does not occur in
equation (
. Because the z coordinate does not occur in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) it remains completely unchanged in the new
coordinate system.
The rescaled z coordinate does trivially affect equation
) it remains completely unchanged in the new
coordinate system.
The rescaled z coordinate does trivially affect equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) by scaling the numerator and denominator equally,
leaving T(0) unchanged.
(h and Vz scale with z, because
they involve the same vertical length units.)
The moveout equation for elliptical anisotropy
thus has the same form as for isotropy; we merely have
to let
by scaling the numerator and denominator equally,
leaving T(0) unchanged.
(h and Vz scale with z, because
they involve the same vertical length units.)
The moveout equation for elliptical anisotropy
thus has the same form as for isotropy; we merely have
to let 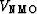 and Vz become independent.
The paraxial moveout velocity
and Vz become independent.
The paraxial moveout velocity 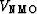 , unaffected
by the stretch in z, must be the horizontal velocity Vx
of the paraxial ellipse.
Because h and Vz can be scaled together with no change in the recorded
traveltimes, the vertical scale in elliptical anisotropy evidently can't be
determined from surface kinematics alone (Dellinger and Muir, 1988).
, unaffected
by the stretch in z, must be the horizontal velocity Vx
of the paraxial ellipse.
Because h and Vz can be scaled together with no change in the recorded
traveltimes, the vertical scale in elliptical anisotropy evidently can't be
determined from surface kinematics alone (Dellinger and Muir, 1988).





Next: THE FIRST ANELLIPTIC APPROXIMATION
Up: Dellinger, Muir, & Karrenbach:
Previous: Introduction
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are usually
not simultaneously available.
Even worse,
the number of parameters required to describe the medium can
be intractably large.
) are usually
not simultaneously available.
Even worse,
the number of parameters required to describe the medium can
be intractably large.
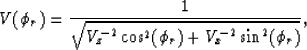
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in terms of
slowness squared M = 1/V2, however,
it simplifies considerably:
) in terms of
slowness squared M = 1/V2, however,
it simplifies considerably:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) displays the fundamental
nature of elliptical anisotropy more clearly.
If you divide equation (
) displays the fundamental
nature of elliptical anisotropy more clearly.
If you divide equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) through by
) through by
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is not accidental.
An ellipse is merely a stretched circle, and
elliptical anisotropy is merely stretched isotropy.
The Fourier similarity theorem
tells us that a ``stretch'' (linear transformation)
in the (x,z) domain corresponds to
an ``inverse stretch'' (another linear transformation)
in the (kx, kz) domain.
Equations (
) is not accidental.
An ellipse is merely a stretched circle, and
elliptical anisotropy is merely stretched isotropy.
The Fourier similarity theorem
tells us that a ``stretch'' (linear transformation)
in the (x,z) domain corresponds to
an ``inverse stretch'' (another linear transformation)
in the (kx, kz) domain.
Equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
look the same because they are both equations for stretched circles,
i.e., ellipses.
)
look the same because they are both equations for stretched circles,
i.e., ellipses.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how elliptical anisotropy can be used as
a first-order paraxial approximation in both the group and phase domains.
Although the group-velocity and phase-slowness representations
of this transversely isotropic medium look very different,
the first-order paraxial approximation is elliptical in both domains.
(The TI medium is Greenhorn Shale from Jones and Wang (1981).)
shows how elliptical anisotropy can be used as
a first-order paraxial approximation in both the group and phase domains.
Although the group-velocity and phase-slowness representations
of this transversely isotropic medium look very different,
the first-order paraxial approximation is elliptical in both domains.
(The TI medium is Greenhorn Shale from Jones and Wang (1981).)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) it remains completely unchanged in the new
coordinate system.
The rescaled z coordinate does trivially affect equation
) it remains completely unchanged in the new
coordinate system.
The rescaled z coordinate does trivially affect equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) by scaling the numerator and denominator equally,
leaving T(0) unchanged.
(h and Vz scale with z, because
they involve the same vertical length units.)
The moveout equation for elliptical anisotropy
thus has the same form as for isotropy; we merely have
to let
by scaling the numerator and denominator equally,
leaving T(0) unchanged.
(h and Vz scale with z, because
they involve the same vertical length units.)
The moveout equation for elliptical anisotropy
thus has the same form as for isotropy; we merely have
to let