Static Shift and Wave-Equation Datuming

The most common form of datuming is to perform static shifts of data traces. This is adequate for regions where the near surface raypaths are nearly vertical and where the shifts are small. The static shift method is commonly applied to correct for near surface velocity variations due to weathering layers, for mild topographic effects, and for differences in shot and geophone elevation. In this section I demonstrate that static shift is inappropriate when the shift is too large because the raypaths are not vertical. I show that downward continuing the data with the wave-equation is a better alternative than static shift when the velocity of the medium is known. Upward continuing the data produces a wavefield which can be correctly imaged although some of the high time-dip information is lost.

Figure 7a shows the migration of the synthetic data from Figure 6a after static shift down to a level datum at the base of the mountain. Similarly, Figure 7b shows the migration of the same synthetic data after shifting upward to a planar datum just above the mountain. In both cases the wavefield is distorted so much by the static shift that the migration fails. The same type of failure occurs for pre-stack data if large static corrections are performed before velocity analysis or any other wave-equation based processing.

 

statmig
Figure 7 (a) Static shift downward followed by migration and (b) static shift upward followed by migration. The process of static shift distorts the wavefield so that migration fails.

The failure of migration or velocity analysis after static shift can be easily understood. Kirchhoff time migration of data collected on a planar surface can be thought of as summation along hyperbolic trajectories Schneider (1978). Figure 8a shows the synthetic data after static shift. This is the data which produced the poor migration in Figure 7b. The diffraction curve from the upper point scatterer is non-hyperbolic and therefore does not collapse to a point after migration. Figure 8b is the same synthetic data propagated upward with the wave-equation datuming algorithm. The diffraction curve due to the scatterer is now hyperbolic. All of the events in Figure 8b are properly positioned.

 

statdat
Figure 8 (a) Static shift upward. (b) Datuming by wave-equation extrapolation upward. Note the difference in curvature of the diffracted events.

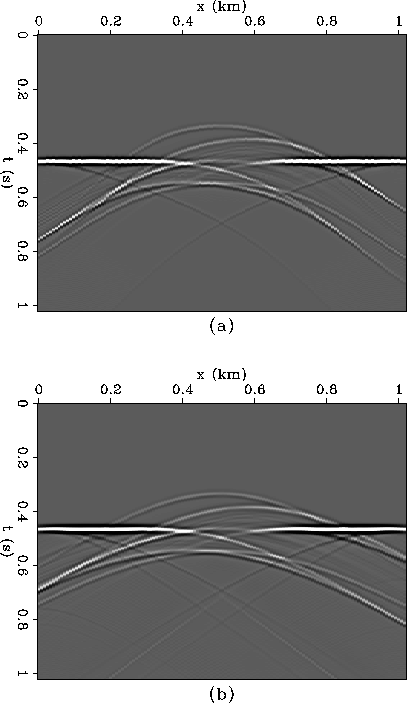Figure 9 shows the migrations of the zero-offset synthetic data after (a) downward continuation and (b) upward continuation. Both produce acceptable images although the image after downward continuation is better since the steep dips are present. When the wavefield is upward continued some of the steep dip information is lost due to limited aperture. Despite these aperture effects the syncline, anticline and diffractors are clearly resolvable in Figure 9b.

 

syndatum
Figure 9 (a) Wave-equation extrapolation downward followed by migration and (b) wave-equation extrapolation upward followed by migration.

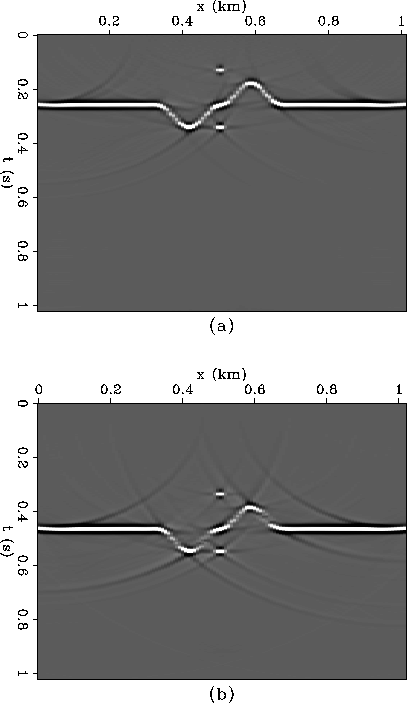Although the result of Figure 9b requires knowledge of the subsurface velocity structure in order to perform the migration, the upward continuation process applied before the migration does not. This implies that data can be upward continued as in Figure 8b with any reasonable velocity. The upward continued data satisfy the wave-equation.