Kirchhoff Modeling and Migration with Topography

A zero-offset Kirchhoff modeling and migration program is used to generate synthetic data on an irregular surface. The algorithm is similar to trimo() Claerbout (1992) but it incorporates topography. The effect of topography is examined by performing static shifts, wave-equation datuming and migration on the zero-offset synthetics. In actual practice data must be datumed pre-stack; However, the zero-offset case is examined here because it is a first step in gaining intuition into the problems encountered with irregular topography and because it is easy to visualize what the zero-offset synthetics should look like. Pre-stack datuming is discussed in a subsequent section.

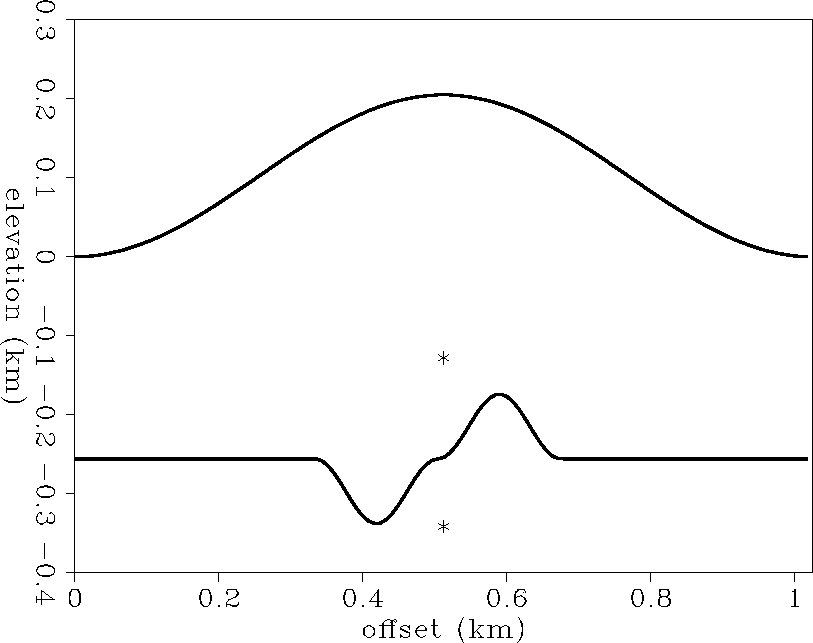
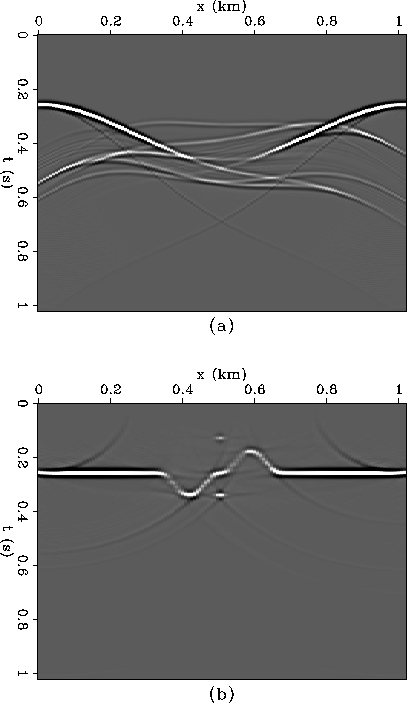
The model used in this section consists of an anticline, a syncline, and two point diffractors in a constant velocity media. The medium velocity is 2 km/s. The topography is modeled as a cosine shaped mountain 200 m high (Figure 5). The effect of the mountain is to create a low frequency undulation which completely distorts the synthetic data (Figure 6a). The data are migrated using the conjugate of the program which created the synthetic (Figure 6b). This type of migration requires knowledge of the subsurface velocity structure. The problem with many land data sets is that the topography distorts the data so much that it is not possible to pick coherent reflection events or to estimate velocity.

 

model Figure 5 Topography and subsurface structure used to generate the zero-offset synthetic data.

 

syn
Figure 6 (a) The zero-offset synthetic data are distorted by the irregular acquisition topography. (b) The synthetic data are migrated using an implicit topographic correction. This requires knowledge of the subsurface velocity structure.