Synthetic Model

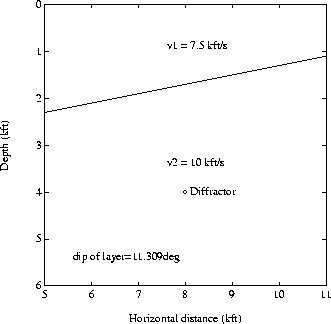
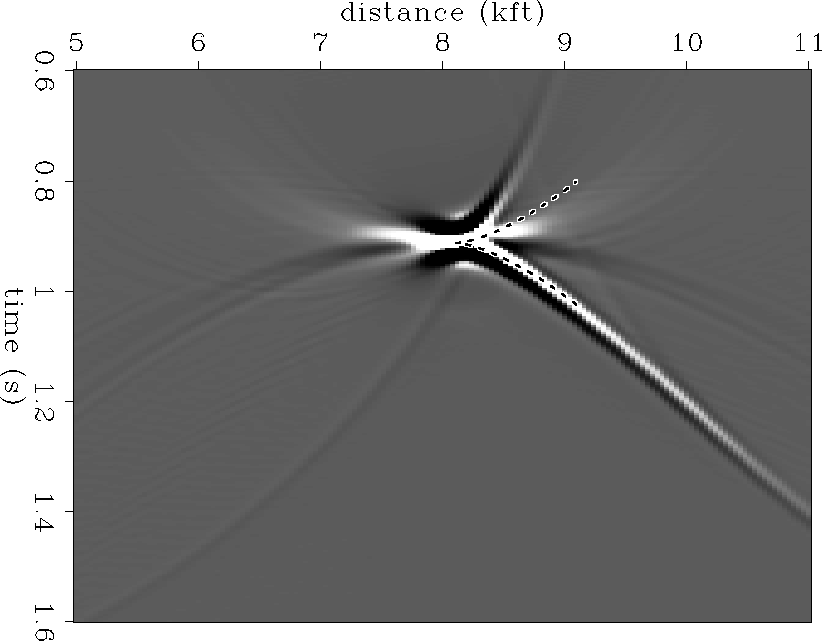
The model used in this paper is the same as that used in Paper 1 (Figure 1). An implicit velocity gradient is caused by the dipping-layer since the velocity changes across it. The plume response due to a point diffractor positioned at a depth of 4 kft at a horizontal position of 8 kft is displayed in Figure 2. This is the Kirchhoff modeling and migration result discussed in Paper 1. The migration velocity is the vertical RMS well velocity of 8.84 kft/s that would be obtained along a well drilled straight down into the diffractor from the surface. The first-order theory derived by Black and Brzostowski 1993 and reviewed in Paper 1 predicts that the plume shape is given by:  

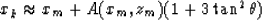$$x_k \approx x_m + A(x_m,z_m)(1+3\tan^2\theta)$$ (1)

 

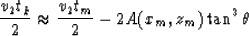$$\frac{v_2t_k}{2} \approx \frac{v_2t_m}{2} - 2A(x_m,z_m)\tan^3\theta$$ (2)

where x_k and t_k are the spatial and temporal coordinates of the time migrated points and 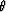$\theta$ is the propagation angle. This is the symmetric curve overlaid on the migration result of Figure 2. As discussed in Paper 1, this theoretical curve accounts for some of the features of the plume but lacks the higher-order terms which account for plume asymmetry.

 

gem1
Figure 1 Dipping-layer model. The change in velocity across the dipping layer causes an implicit velocity gradient which depends on the dip of the layer.

 

analytic
Figure 2 Comparison of the analytic expression for the plume to the Kirchhoff migration result.