




Next: THE SPLIT-STEP FOURIER MODELING
Up: Popovici : PSPI and
Previous: INTRODUCTION
The derivation of the Phase Shift Plus Interpolation (PSPI) modeling
algorithm
starts with the scalar wave equation
| 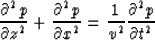 |
(1) |
where p=p(x,z,t) is the pressure field and v=v(x,z) is the earth
velocity.
The pressure field p(x,z,t) is a finite function and can be therefore
expressed as a double Fourier series
| 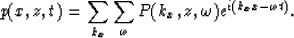 |
(2) |
Substituting equation (2) in equation (1) we obtain
| ![\begin{displaymath}
{\sum_{k_x} \sum_{\omega}[ {\partial^2 P(k_x,z,\omega) \over...
...a^2 \over v^2(x,z)} P(k_x,z,\omega)]
e^{i(k_x x-\omega t)}= 0}.\end{displaymath}](img3.gif) |
(3) |
Equation (3) should hold for any values of kx and 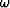 .This is possible only if each term inside the square parenthesis
is zero. This reasoning is similar to the condition that if
a polynomial is zero for any values of x, the coefficients of the
polynomial are zero.
Equation (3) becomes
.This is possible only if each term inside the square parenthesis
is zero. This reasoning is similar to the condition that if
a polynomial is zero for any values of x, the coefficients of the
polynomial are zero.
Equation (3) becomes
| 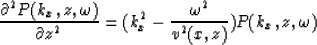 |
(4) |
valid for all values of kx and 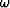 .The problem is that in this form, the x-coordinate in the pressure
field is Fourier transformed and there is no direct
correspondence between a point (x,z) in the medium,
the velocity v(x,z), and the corresponding value of p(x,z,t)
at that location.
.The problem is that in this form, the x-coordinate in the pressure
field is Fourier transformed and there is no direct
correspondence between a point (x,z) in the medium,
the velocity v(x,z), and the corresponding value of p(x,z,t)
at that location.
For a constant velocity we write
| ![\begin{displaymath}
k_z={\pm {[{\omega^2 \over v^2}-{k^2_x }]^{1 \over 2}}}\end{displaymath}](img6.gif) |
(5) |
where kz is constant for two given values of kx and 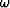 .Equation (5) is the well known dispersion
relation.
Equation (4) becomes an ordinary differential equation
.Equation (5) is the well known dispersion
relation.
Equation (4) becomes an ordinary differential equation
| 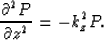 |
(6) |
For a constant kz equation (6) has the analytic solution
| 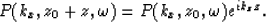 |
(7) |
Equation (7) shows how in constant velocity media we
can find the pressure field at a certain depth level 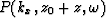 ,
if we know it at any other depth level
,
if we know it at any other depth level 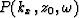 .
.
However there are several ambiguities in equation (7)
that we need to discuss.
One is the question of time propagation. If we know the
pressure field (or wavefield) at a certain depth we can
propagate it forward in time or backward in time. We
can also propagate it up (along the z-axis) or down.
To understand how we determine the propagation direction
we have to analyze the values and
sign of kz.
There are several restrictions on the values of kz. Equation
(6) has the solution (7) only for real
values of kz which imposes the condition
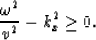
The solution represented in equation (7) is the
Fourier transform of the wavefield. The general solution
in time-space coordinates is obtained by summing all the
Fourier coefficients obtained from equation (7)
| 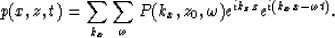 |
(8) |
The function
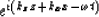
represents a plane wave. Equation (8) sums
many plane waves to obtain the general solution.
We examine the sign of kz necessary to upward
propagate a wave by examining each plane wave solution.
If we ignore kx x, which determines the lateral variation,
we can write
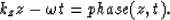
The phase is constant along a plane wave, and we write
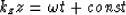
for the phase of a particular plane wave.
The plane wave is moving downward when kz has the
same sign with 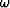 because z increases with t
in order to keep the phase constant. So for the upward
moving waves we need to have opposite signs of kz and
because z increases with t
in order to keep the phase constant. So for the upward
moving waves we need to have opposite signs of kz and 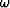 (z is decreasing when t is increasing).
We have now figured out that in order to have only upgoing
waves we have to look at the sign of
(z is decreasing when t is increasing).
We have now figured out that in order to have only upgoing
waves we have to look at the sign of 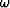 and assign to
kz the opposite sign.
and assign to
kz the opposite sign.
Next we correlate this information
with the depth level where we want to find the wavefield.
If the known wavefield is at depth z0 and we want to
find the wavefield at depth z0+z, then we have
to propagate the wavefield back in time (toward t=0)
because we know that the wavefield travels upward.
If the known wavefield is at depth z0 and we want to
find the wavefield at depth z0-z, then we are
propagating the wavefield forward in time. This is the
direction we are interested in for modeling.
However for depth varying velocity v(z) we have kz
approximately constant only
for small depth intervals (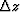 ) where we can consider the velocity constant.
Therefore equation (7) becomes
) where we can consider the velocity constant.
Therefore equation (7) becomes
| 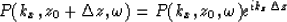 |
(9) |
and can be used to downward or upward extrapolate
the wave field for a small depth interval.
For laterally variant media, Gazdag and Sguazzero (1984) propose to downward
extrapolate the wavefield one depth interval at a time with several
velocities. We can apply the same idea to upward propagate the
wavefield with several velocities.
We consider
several velocities (v1, v2, ...) in the interval
[vmin,vmax] and upward propagate the wavefield
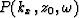 to
to 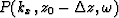 with
each velocity.
We can afterward inverse Fourier transform in x the resulting wavefields
with
each velocity.
We can afterward inverse Fourier transform in x the resulting wavefields
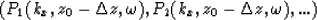
to obtain
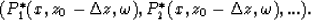
To obtain a single upward propagated
wavefield, at each point 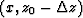 associated with a velocity
associated with a velocity 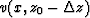 ,
the value of the resulting wavefield
in this point is interpolated between the two wavefields with
closest velocities (
,
the value of the resulting wavefield
in this point is interpolated between the two wavefields with
closest velocities (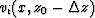 ).
).
In addition we need to implement a technique (Gazdag and Sguazzero, 1984) in the
PSPI modeling algorithm to ensure that all the zero dips (corresponding to the
case kx=0) are upward propagated without distortion. The technique
consists of multiplying the wavefield 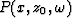 with
with
| 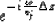 |
(10) |
after the Fourier transformation in x
and multiplying the upward propagated wavefield
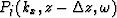 by
by
| 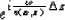 |
(11) |
where
the subscript j denotes the index of the constant velocity used in the
upward propagation step.
For a zero dip plane wave (i.e. kx = 0) we have
| 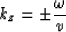 |
(12) |
and the plane wave can be upward propagated with the velocity
v(x,z) corresponding to the point coordinates (x,z) instead
of the constant velocity vj.
As it will be seen later when the PSPI results are
compared to the Split-step Fourier results, this supplemental
phase subtraction and addition improves the accuracy in the migration
case but actually produces worse results in the modeling case.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the flow of the
PSPI migration and modeling algorithms.
shows the flow of the
PSPI migration and modeling algorithms.
pspiboth
Figure 1 Phase Shift Plus Interpolation (PSPI) migration and the
conjugate transpose PSPI modeling algorithm.






Next: THE SPLIT-STEP FOURIER MODELING
Up: Popovici : PSPI and
Previous: INTRODUCTION
Stanford Exploration Project
11/18/1997
![]()
![]()
![]()
![]()
![]() ) where we can consider the velocity constant.
Therefore equation (7) becomes
) where we can consider the velocity constant.
Therefore equation (7) becomes
![]() to
to ![]() with
each velocity.
We can afterward inverse Fourier transform in x the resulting wavefields
with
each velocity.
We can afterward inverse Fourier transform in x the resulting wavefields
![]()
![]()
![]() with
with
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the flow of the
PSPI migration and modeling algorithms.
shows the flow of the
PSPI migration and modeling algorithms.
