RATIONALE

Gardner's approach to constant velocity DMO transforms the nonzero offset data cube into an output cube with an artificial offset k and traveltime t₁. After NMO and poststack migration an input impulse results in an output data cube which depicts the corresponding ellipsoidal surface. The transformation is defined by:

 

k² = h²-b²,

 

$$t_{1} = {t_{n}{k}\over{h}},$$ (2)

 

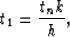$$t_{0} = {t^{2}_{1}}-{4 k^{2}\over{V^{2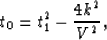}}},$$ (3)

where t_n and h are the traveltime and offset of the original data input trace, and b is the distance between the replacement trace's midpoint and the input trace's midpoint. t₀ is the desired zero offset traveltime at b, k is defined by equation (1). Equation (3) shows t₀ to be the NMO corrected time for offset k using the moveout velocity V. Transformations (1) and (2) are velocity independent. The final NMO step (3) permits a standard velocity analysis.

Equations (1) and (2) define the DMO operator, which in the input data set is a slanting hyperbola, lying in the radial plane. The DMO operation sums along this hyperbola and stores the sum at the hyperbola's vertex. The impulse responses of the DMO process are slanting semicircles.