




Next: Convolution in constant frequency
Up: RATIONALE
Previous: RATIONALE
To realize transformation (2) each input trace, q(t,m,h), has to
be stretched by the factor k/h:
| 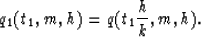 |
(4) |
The differential time moveout 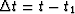 of equation (1) is
proportional to time:
of equation (1) is
proportional to time:
| 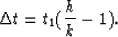 |
(5) |
Logarithmic resampling is defined by:
| 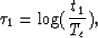 |
(6) |
where 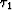 denotes the frequency variable after Fourier transformation
of the input trace. Tc is the start of the unmuted frequency trace.
Elsewhere in this report (), I show that
After two Fourier transforms and the intermediate logarithmic
resampling, each trace stretching amounts to a simple
trace scaling:
denotes the frequency variable after Fourier transformation
of the input trace. Tc is the start of the unmuted frequency trace.
Elsewhere in this report (), I show that
After two Fourier transforms and the intermediate logarithmic
resampling, each trace stretching amounts to a simple
trace scaling:
| 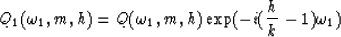 |
(7) |
Resampling the Fourier transformed input trace rather than
the trace itself takes advantage of the band limitation of typical
seismic data ().
The more compact data cube reduces the computation time and
the amount of memory required.





Next: Convolution in constant frequency
Up: RATIONALE
Previous: RATIONALE
Stanford Exploration Project
11/18/1997