A Kirchoff based kinematic scheme

Berryhill presents a simple algorithm based on the Kirchoff integral to perform the wavefield transformation from one datum (U(x,z=z₁ ,t)) to another (U(x,z=z₂ ,t)) Each individual trace U_j (t) comprising U(x,z=z₂ ,t) is calculated by performing the sum:  

$${U_j (t)= \sum_j \triangle x_i cos \theta_i {t_i \over r_i} Q_i(t-t_i)}$$ (1)

where Q_i(t-t_i) is a filtered input trace recorded at location i and delayed by traveltime t_i. $\triangle x_i$ is the input trace interval, $\theta_i$ is the angle between the normal to the surface at z=z₂ and the line r_i connecting U_j and U_i. The geometry of the transformation is illustrated in Figure . A complete derivation of this equation is presented in Berryhill 1979.

 

datum Figure 1 Geometry for the continuation of a wavefield between an irregular topography and a planar datum (after Berryhill, 1984)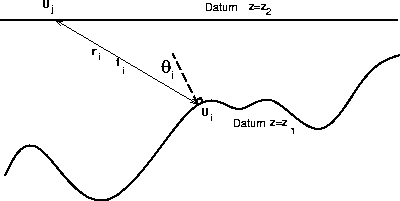

My proposed method may be summerized in three steps:

• Extrapolate the data upwards to a flat datum (by using equation ( 1)). This should unravel the distortions caused by the irregular acquisition topography.
• Perform velocity analysis at the flat datum. This determines the near-surface velocity structure.
• Either perform the processing and imaging or extrapolate downward to some flat datum below the acquisition topography.