




Next: About this document ...
Up: Zhang: F-D calculation
Previous: APPENDIX A
To derive equation (16), I take the derivative of both
sides of equation (15) with respect to s and map the
result to Cartesian coordinates, which yields
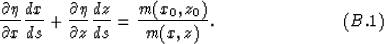
The ray equation (6) gives
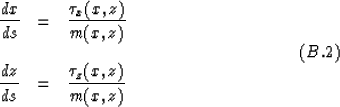
Substituting these relations from equation (B.2) into equation (B.1)
and multiplying both sizes by m(x,z) yields equation (16):
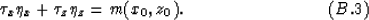
When (x,z) tends to (x0,z0), s tends to s0 and  tends to zero,
which gives the initial condition.
tends to zero,
which gives the initial condition.





Next: About this document ...
Up: Zhang: F-D calculation
Previous: APPENDIX A
Stanford Exploration Project
12/18/1997
![]()
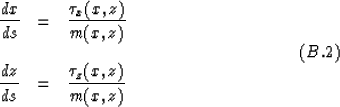
![]()