




Next: EXAMPLES
Up: LINEAR OPTIMIZATION
Previous: Objective function
As two neighboring traces will not always be matched perfectly just by
shifting, it is useful to define some quantity that measures the quality
of the picking process.
This quantity will have its value between and 1. It will equal
to when input is all-zero or white noise, equal to 1 when the
matching can be made perfectly.
In the plane-wave destructor method, Claerbout (1990) chose
the normalized correlation of the partial derivatives of data as a measure.
Here, we will use the normalized correlation of data itself:
| 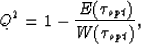 |
(10) |
where
![\begin{displaymath}
W(\tau)={1 \over N}\sum^N_t\left\{
{1 \over \Vert u^2_1(t) \...
...{1 \over \Vert u^2_2(t) \Vert}[u^2_2(t)+u^2_1(t-\tau)]\right\}.\end{displaymath}](img27.gif)
By inserting 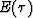 in equation (3) into this definition,
we have
in equation (3) into this definition,
we have
| ![\begin{displaymath}
Q=\sqrt{\displaystyle{{2\sum^N_t\left[
{1 \over \Vert u^2_1(...
...\Vert u^2_2(t) \Vert}[u^2_2(t)+u^2_1(t-\tau_{opt})]\right\}}}}.\end{displaymath}](img29.gif) |
(11) |
The computations of the linear optimization and the quality measure
can be done in a similar way to that of the nonlinear optimization.
The code vectorizes fully.





Next: EXAMPLES
Up: LINEAR OPTIMIZATION
Previous: Objective function
Stanford Exploration Project
1/13/1998
![\begin{displaymath}
W(\tau)={1 \over N}\sum^N_t\left\{
{1 \over \Vert u^2_1(t) \...
...{1 \over \Vert u^2_2(t) \Vert}[u^2_2(t)+u^2_1(t-\tau)]\right\}.\end{displaymath}](img27.gif)
![\begin{displaymath}
Q=\sqrt{\displaystyle{{2\sum^N_t\left[
{1 \over \Vert u^2_1(...
...\Vert u^2_2(t) \Vert}[u^2_2(t)+u^2_1(t-\tau_{opt})]\right\}}}}.\end{displaymath}](img29.gif)