




Next: Algorithm
Up: NON-LINEAR OPTIMIZATION
Previous: NON-LINEAR OPTIMIZATION
Suppose u1(t) and u2(t) are two traces of seismic data u(t,x):

with 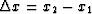 being the distance between the two traces.
We want to construct an objective function that measures the misfitting
of two traces when they are shifted relative to one another.
The standard least squares method suggests the following two expressions
being the distance between the two traces.
We want to construct an objective function that measures the misfitting
of two traces when they are shifted relative to one another.
The standard least squares method suggests the following two expressions
| ![\begin{displaymath}[u_1(t)-u_2(t+\tau)]
^2 \ \ \ \ \hbox{or} \ \ \ \ [u_2(t)-u_1(t-\tau)]^2.\end{displaymath}](img7.gif) |
(2) |
These two expressions are useful when seismic data is adequately sampled
along the spatial axis. However, when data is aliased, these expressions
as the functions of  , have many local minima, as shown in
Figure 1c.
This may lead to a totally wrong estimate of the time-shift
, have many local minima, as shown in
Figure 1c.
This may lead to a totally wrong estimate of the time-shift  .
The solution to this problem is to use some special information of data
as constraints to reduce, or even to remove, the ambiguities.
.
The solution to this problem is to use some special information of data
as constraints to reduce, or even to remove, the ambiguities.
There are many ways to constrain the solutions. The two
commonly used methods are: adding extra terms to the objective
function and multiplying weighting functions to the objective function.
The method of adding extra terms can possibly
preserve some of the important properties of the objective function, such
as quadratic forms. But the relative weights between the two terms of the
objective function are not easy to determine. The weighting method
does not have this problem. But it will make the objective function
non-quadratic when the weighting function are data-dependent. Since the
expressions in equation (2) are not quadratic functions of
time-shift  anyway (thought they are quadratic functions of data),
the weighting function method is apparently easy to apply.
anyway (thought they are quadratic functions of data),
the weighting function method is apparently easy to apply.
Human eyes can eliminate the aliasing effects
on dip-picking by
looking at the amplitude information of data, especially the breaks
of first arrivals. This suggests using the following objective function:
| ![\begin{displaymath}
E(\tau)={1 \over N} \sum^N_t\left\{
{1 \over \Vert u^2_1(t)\...
...2
{1 \over \Vert u^2_2(t)\Vert }[u_2(t)-u_1(t-\tau)]^2\right\},\end{displaymath}](img8.gif) |
(3) |
where 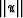 represents the smoothed version of u, and the summation
is undertaken in the neighborhood of point (t,x). The reason to
choose this kind of weighting function is clearly shown in
Figures 1a and 1b.
The penality is extremely large when the first
breaks of traces do not match with each other. Figures 1a and
1b
also show why both expressions in equation (2) must be
included in the objective function. Figures 1c and
1d show that after
the weighting functions are applied, false local minima become less ambiguous.
objill
represents the smoothed version of u, and the summation
is undertaken in the neighborhood of point (t,x). The reason to
choose this kind of weighting function is clearly shown in
Figures 1a and 1b.
The penality is extremely large when the first
breaks of traces do not match with each other. Figures 1a and
1b
also show why both expressions in equation (2) must be
included in the objective function. Figures 1c and
1d show that after
the weighting functions are applied, false local minima become less ambiguous.
objill
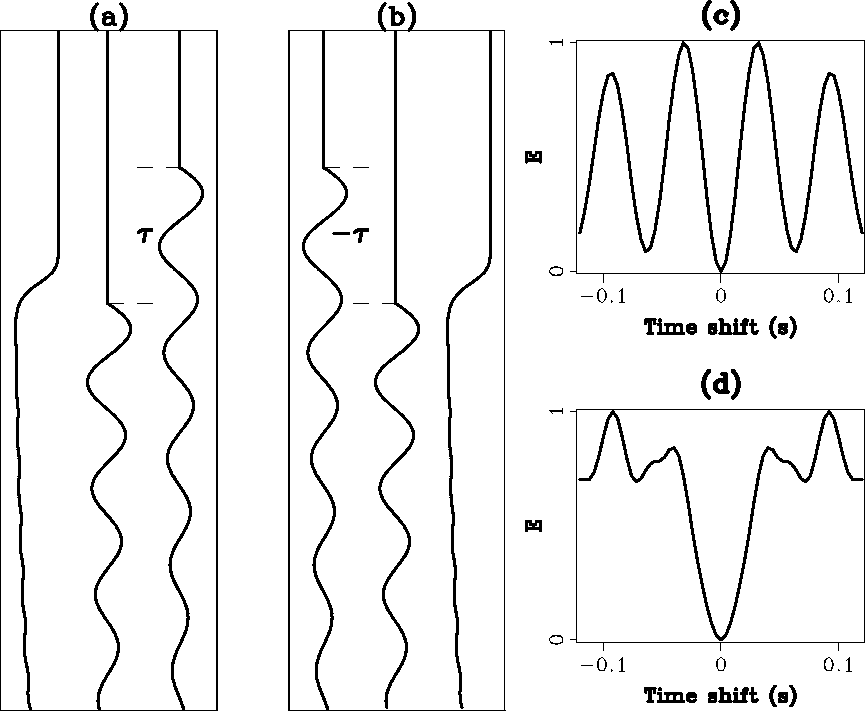
Figure 1 Illustrations of the objective function: (a) three traces are
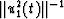 , u1(t) and
, u1(t) and 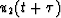 from left to right,
the weighting function
from left to right,
the weighting function
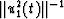 causes the penalty to be extremely
high when
causes the penalty to be extremely
high when  is not zero; (b) similar to (a) where three traces are
is not zero; (b) similar to (a) where three traces are
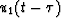 , u2(t) and
, u2(t) and 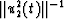 ; (c) the objective
function computed from traces in (a) and (b) without the weighting functions,
it has several suspicious minima; (d) the objective function
with the weighting functions, suspicious minima are lifted up.
; (c) the objective
function computed from traces in (a) and (b) without the weighting functions,
it has several suspicious minima; (d) the objective function
with the weighting functions, suspicious minima are lifted up.

An alternative form of the objective function is
| ![\begin{displaymath}
Q(p)={1 \over N} \sum^N_t\left\{
{1 \over \sqrt{\Vert u^2_1(...
...ert }}
[u_1(t-{\tau \over 2})-u_2(t+{\tau \over 2})]^2 \right\}\end{displaymath}](img14.gif) |
(4) |
which has one term and displays better symmetry around time t. But
the disadvantage of this form is that the weighting function is
 -dependent.
-dependent.





Next: Algorithm
Up: NON-LINEAR OPTIMIZATION
Previous: NON-LINEAR OPTIMIZATION
Stanford Exploration Project
1/13/1998
![]()
![]() anyway (thought they are quadratic functions of data),
the weighting function method is apparently easy to apply.
anyway (thought they are quadratic functions of data),
the weighting function method is apparently easy to apply.
![\begin{displaymath}
E(\tau)={1 \over N} \sum^N_t\left\{
{1 \over \Vert u^2_1(t)\...
...2
{1 \over \Vert u^2_2(t)\Vert }[u_2(t)-u_1(t-\tau)]^2\right\},\end{displaymath}](img8.gif)
![\begin{displaymath}
Q(p)={1 \over N} \sum^N_t\left\{
{1 \over \sqrt{\Vert u^2_1(...
...ert }}
[u_1(t-{\tau \over 2})-u_2(t+{\tau \over 2})]^2 \right\}\end{displaymath}](img14.gif)