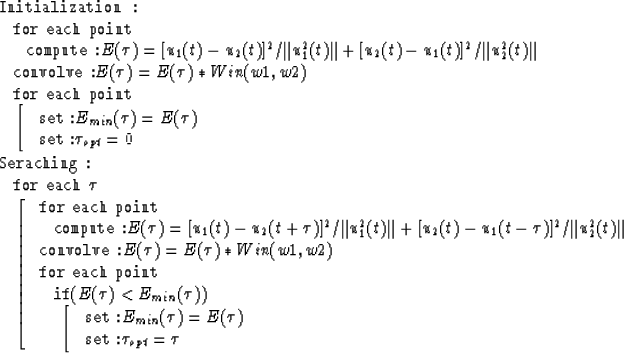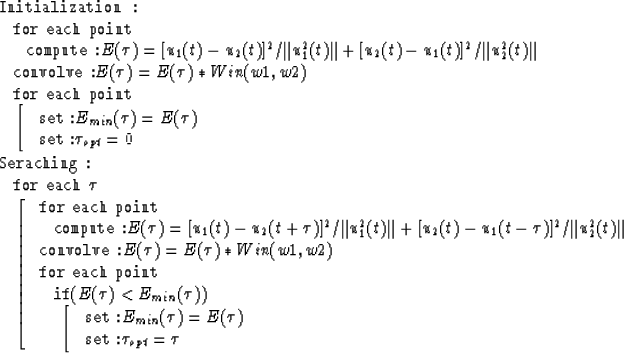Next: LINEAR OPTIMIZATION
Up: NON-LINEAR OPTIMIZATION
Previous: Objective function
Up till now, we have treated  as a constant. In the real world, however,
the seismic reflections are almost always curved events. Therefore,
as a constant. In the real world, however,
the seismic reflections are almost always curved events. Therefore,
 changes its value from place to place. To deal with this
nonstationarity, we consider the curved events as piecewise linear and
chop a seismic section into many subsections. The optimal
changes its value from place to place. To deal with this
nonstationarity, we consider the curved events as piecewise linear and
chop a seismic section into many subsections. The optimal  in a subsection
is the minimizer of the objective function that is computed from the data
samples in the subsection. This is a one-dimensional
non-linear optimization problem and can be conveniently solved by
searching. A straight forward implementation of the algorithm is
to read the data samples in a subsection, then to compute
the objective function
for all possible
in a subsection
is the minimizer of the objective function that is computed from the data
samples in the subsection. This is a one-dimensional
non-linear optimization problem and can be conveniently solved by
searching. A straight forward implementation of the algorithm is
to read the data samples in a subsection, then to compute
the objective function
for all possible  , and finally to find the
, and finally to find the  that minimizes the
objection function. These steps are repeated for every subsection.
This implementation is actually cumbersome and computationally
expensive because many boundaries must be properly handled and
the objective function may be computed more than once at the points
shared by several subsections.
that minimizes the
objection function. These steps are repeated for every subsection.
This implementation is actually cumbersome and computationally
expensive because many boundaries must be properly handled and
the objective function may be computed more than once at the points
shared by several subsections.
We have found an efficient way to implement the algorithm. The scheme of
the implementation is:
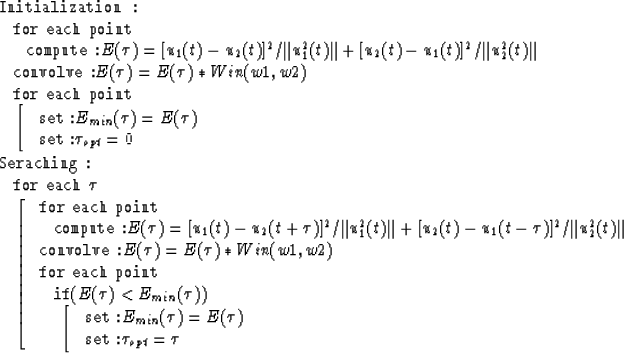
The only kind of boundaries that the program has to deal with is the
truncation of data, but it can be easily handled by padding zeros.
The code of this implementation vectorizes fully.





Next: LINEAR OPTIMIZATION
Up: NON-LINEAR OPTIMIZATION
Previous: Objective function
Stanford Exploration Project
1/13/1998