




Next: The quality of picking
Up: LINEAR OPTIMIZATION
Previous: LINEAR OPTIMIZATION
Let 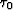 be an estimate of the relative time-shift obtained through
the non-linear optimization. We assume the true solution is
be an estimate of the relative time-shift obtained through
the non-linear optimization. We assume the true solution is
| 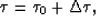 |
(5) |
where 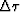 is a residual time-shift. We will estimate
is a residual time-shift. We will estimate 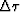 by solving a linear optimization problem. First, we linearize the model.
and
Then we substitute these expressions into equation (3). The
new objective function becomes a quadratic function of the unknown
by solving a linear optimization problem. First, we linearize the model.
and
Then we substitute these expressions into equation (3). The
new objective function becomes a quadratic function of the unknown
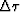 :
:
| ![\begin{displaymath}
\begin{array}
{lll}
\hat{E}(\Delta \tau) & = & {1 \over N} \...
...\tau_0)+u^\prime_1(t-\tau_0)\Delta \tau]^2
\right\}.\end{array}\end{displaymath}](img21.gif) |
(6) |
The optimal estimation of 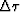 is obtained by finding the minimizer
of
is obtained by finding the minimizer
of 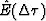 . The standard least squares technique gives
. The standard least squares technique gives
| ![\begin{displaymath}
\Delta \tau = -\displaystyle{{\sum^N_t\left\{
{1 \over \Vert...
...\over \Vert u^2_2(t) \Vert}[u^\prime_1(t-\tau_0)]^2 \right\}}}.\end{displaymath}](img23.gif) |
(7) |
This solution looks similar in expression to the solution of the
plane-wave destructor. It actually has two distinguished features.
First it includes weighting functions. Second, it does not
require to compute the
partial derivatives of data with respect to the spatial axis, which is
difficult to do in high accuracy when spatial-sample interval is large.
The second feature comes from the fact that we estimate the relative
time-shifts instead of the dips.
The computation of the time-derivatives of data is not a problem as we have
assumed that data is adequately sampled in the time axis.
Thus, the overall optimal relative time-shift is
| 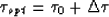 |
(8) |
and the optimal dip is
| 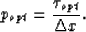 |
(9) |
Clearly the linear optimization can be run iteratively. Examples with
synthetic and field data show that first iteration provides a solution
of sufficient accuracy.





Next: The quality of picking
Up: LINEAR OPTIMIZATION
Previous: LINEAR OPTIMIZATION
Stanford Exploration Project
1/13/1998
![]() be an estimate of the relative time-shift obtained through
the non-linear optimization. We assume the true solution is
be an estimate of the relative time-shift obtained through
the non-linear optimization. We assume the true solution is
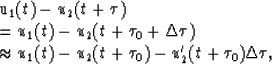
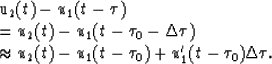
![\begin{displaymath}
\begin{array}
{lll}
\hat{E}(\Delta \tau) & = & {1 \over N} \...
...\tau_0)+u^\prime_1(t-\tau_0)\Delta \tau]^2
\right\}.\end{array}\end{displaymath}](img21.gif)
![\begin{displaymath}
\Delta \tau = -\displaystyle{{\sum^N_t\left\{
{1 \over \Vert...
...\over \Vert u^2_2(t) \Vert}[u^\prime_1(t-\tau_0)]^2 \right\}}}.\end{displaymath}](img23.gif)