




Next: GENERATION OF SURFACE VALUES
Up: THE GENERALIZED PHASE-SHIFT METHOD
Previous: Arbitrary velocity structures
When the velocity structure varies arbitrarily in the lateral direction,
the eigenvalues and eigenvectors of matrix A can no longer be obtained by
inspection. It would therefore seem that a matrix diagonalization would
have to be performed before each propagation to equation (11). However,
recent work by Tal-Ezer(1986) indicates how the calculation of
matrix exponential can be done without having to resort to expensive
matrix diagonalizations.
The solution is based on a Chebychev expansion for the function ex given by
| 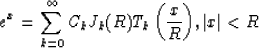 |
(18) |
where x is imaginary and C0=1 and Ck=2 for k>0.
The polynomials Tk(x) satisfy the recurrence relations
T0(x) = 1,
T1(x) = x,
and
Tk+1(x)=Tk-1(x)+2xTk(x)
(Tal-Ezer, 1986). By analogy with equation (18), the exponent in
equation (4) is expanded according to
| 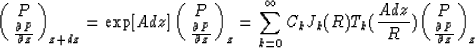 |
(19) |
This expansion is valid when the eigenvalues of [Adz] are purely imaginary
and R must be chosen large enough to span the range of the eigenvalues of
[Adz]. It was shown in Tal-Ezer(1986) that for k > R, the series expansion
converges exponentially. The number of terms required in the sum in
equation (19) will therefore always be finite.
Equation (19) serves as the basis for implementing the generalized phase-shift
migration. First the range R of the eigenvalues of [Adz] need to be
estimated.
Based on the case of laterally uniform velocity, Kosloff showed the estimate
r=wdz/cmin with cmin denoting the lowest velocity in the strip
(z,z+dz), is sufficient for stable results. The Bessel functions Jk(R) are
computed next.
The solution
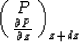
is then calculated recursively according to following:
The first two values of T0, T1 needed to initialize the recursion are
given by
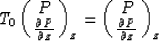
and
![\begin{displaymath}
T_1\pmatrix { P \cr {\partial P\over \partial z}}_z= [{Adz \over R}]\pmatrix { P \cr {\partial P\over \partial z}}_z\end{displaymath}](img36.gif)
The next polynomial is generated by the recursion formula
![\begin{displaymath}
T_{k+1}\pmatrix { P \cr {\partial P\over \partial z}}_z= T_{...
...dz \over R}]T_k\pmatrix { P \cr {\partial P\over \partial z}}_z\end{displaymath}](img37.gif)
These steps are repeated until a sufficient number of terms have been calculated
in the sum(19). Then the solution is carried out in the next lower level.
When 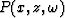 has been calculated completely, the final migrated
section is cumulated by
has been calculated completely, the final migrated
section is cumulated by
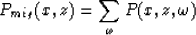
(Kosloff and Baysal, 1983).





Next: GENERATION OF SURFACE VALUES
Up: THE GENERALIZED PHASE-SHIFT METHOD
Previous: Arbitrary velocity structures
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()
![]()
![]()