




Next: Horizontally Uniform Structures
Up: Ji: generalized phase-shift method
Previous: Introduction
The generalized phase-shift method is based on the solution of the temporally
transformed acoustic wave equation
| 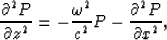 |
(1) |
where 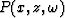 denotes the temporal transform of the pressure field and
c(x,z)
is velocity field. As suggested by Kosloff and Baysal(1983), it is convenient to
recast equation (1) as a set of two first-order coupled equations given by
denotes the temporal transform of the pressure field and
c(x,z)
is velocity field. As suggested by Kosloff and Baysal(1983), it is convenient to
recast equation (1) as a set of two first-order coupled equations given by
| 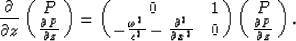 |
(2) |
The downward continuation in the migration consists of the solution of equation
(2) for each frequency at all depths under the initial conditions of the values of P
and 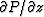 at the surface z=0 (Kosloff and Baysal, 1983).
Equation (2) can be expressed in a more compact form
at the surface z=0 (Kosloff and Baysal, 1983).
Equation (2) can be expressed in a more compact form
| ![\begin{displaymath}
{\partial \over \partial z} \pmatrix{P\cr {\partial P\over \partial z}} = [A]\pmatrix{P\cr {\partial P\over \partial z}},\end{displaymath}](img5.gif) |
(3) |
where ![$[ P ,{\partial P / \partial z}]^T$](img6.gif) denotes a column vector of length
2Nx containing first the Nx pressures
denotes a column vector of length
2Nx containing first the Nx pressures 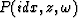 and then the
Nx pressure derivatives
and then the
Nx pressure derivatives ![${\partial / \partial z} [P(idx,z,\omega)]$](img8.gif) ,
for i=0,...,Nx-1.
As with the ordinary phase-shift method, the solution here is propagated in
depth increments. Within each increment z to z+dz, the velocity is assumed
to be invariant in the vertical direction although it may vary horizontally.
The solution of equation (3) can then be written as
,
for i=0,...,Nx-1.
As with the ordinary phase-shift method, the solution here is propagated in
depth increments. Within each increment z to z+dz, the velocity is assumed
to be invariant in the vertical direction although it may vary horizontally.
The solution of equation (3) can then be written as
| ![\begin{displaymath}
\pmatrix{P\cr {\partial P\over \partial z}}_{z+dz} = \exp[Adz]\pmatrix{P\cr {\partial P\over \partial z}}_z.\end{displaymath}](img9.gif) |
(4) |
The solution (4) embodies a phase-shift of the eigenvector coefficients of A.
It would therefore seem that a matrix diagonalization would have to be
performed before each propagation.





Next: Horizontally Uniform Structures
Up: Ji: generalized phase-shift method
Previous: Introduction
Stanford Exploration Project
1/13/1998