| 2|c|Table 2: Fourier Transformations | |
| e-| t | | |
| e-t.H(t) | |
| H(t) | |
| t e-t.H(t) |
| 2|c|Table 2: Fourier Transformations | |
| e-| t | | |
| e-t.H(t) | |
| H(t) | |
| t e-t.H(t) |
It is very simple to determine the Fourier transforms of all the functions in Table 1 using these simple properties of the Fourier transformation:
![\begin{eqnarraystar}
f(at) & \longleftrightarrow & {1\over \vert a\vert}F({\omeg...
... & {1\over 2}[F(\omega +\omega_{0}) + F(\omega -\omega_{0})]. \end{eqnarraystar}](img26.gif) |
||
We can see from the Table 2 that the Fourier transforms of functions with
discontinuities of order 0 behave at ![]() as
as ![]() .Meanwhile, in case of a discontinuity of order 1,
.Meanwhile, in case of a discontinuity of order 1, ![]() behaves
asymptotically as
behaves
asymptotically as ![]() . Let us take, for instance, the third function
from Table 1:
. Let us take, for instance, the third function
from Table 1: ![]() . In this case,
. In this case, ![]() where
where ![]() Then
Then
![\begin{displaymath}
G({\omega}) = {\bf F}_{t}g(t)={1 \over 2i\alpha}
\left[ {1-i...
...over 1 + {({{\omega}+ {\omega}_{0} \over \alpha})}^{2}} \right]\end{displaymath}](img34.gif)
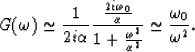
We shall prove the following statement. Let f(t) be a right-sided function,
and, let's suppose that, for all ![]() ,
, ![]() (when
(when ![]() ) in the same way as exp
) in the same way as exp ![]() . Then:
. Then:
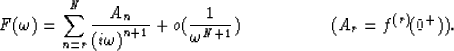 |
(2) |
As f(t) is a right-sided function, we have:
| |
(3) |
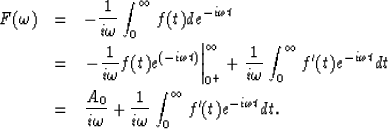 |
(4) | |
| (5) | ||
| (6) |
Repeating this N times we obtain
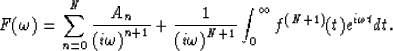 |
(7) |
By definition of the order of discontinuity ![]() . From the condition concerning the behavior of f(k)(t) at
. From the condition concerning the behavior of f(k)(t) at ![]() , the integral on the righthand side of equation (7) converges to at
, the integral on the righthand side of equation (7) converges to at ![]() . This means that the last equation is equivalent to
equation (2).
So the asymptotic behavior of the Fourier-transforms for high frequencies
reflects the sharpness of the discontinuities of the (original) functions.
Both notions (asymptotic behavior and discontinuities) are equivalent ones.
. This means that the last equation is equivalent to
equation (2).
So the asymptotic behavior of the Fourier-transforms for high frequencies
reflects the sharpness of the discontinuities of the (original) functions.
Both notions (asymptotic behavior and discontinuities) are equivalent ones.