




Next: Discontinuities and high-frequency band
Up: 2: THE STANDARD DISCONTINUITIES
Previous: Fourier-transformation
It follows directly from convolution theorem and Formula 15 that
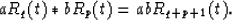
Moreover, if 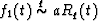 and
and
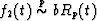 , then
, then
| 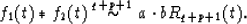 |
(16) |
Proof: Let us express Fourier-transformations of f1(t) and f2(t)
according to equation (2),
taking N=r=q (for f1(t)) and N=r=p
(for f2(t)). Performing multiplication, we get:
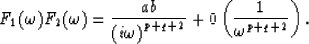
That is exactly the same that equation (16) expresses in temporal domain.
The convolution
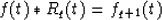
is the qth integration of the f(t).





Next: Discontinuities and high-frequency band
Up: 2: THE STANDARD DISCONTINUITIES
Previous: Fourier-transformation
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()