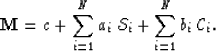
I use here an approach that is closely related to this second form, but which substantially simplifies the forward computations in the initial iterations. Moreover, because of the way it builds the solution- by the introduction of successive degrees of complexity, this method is highly stable.
Similarly to the Fourier decomposition, the method represents the sloth model as composed by the superposition of two sets of oscillatory functions (one set comprised of symmetric functions and the other comprised of anti-symmetric functions), plus a constant factor that accounts for the average-model
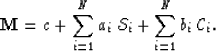 |
(5) |
The first step of the method corresponds to the homogeneous
inversion described in the previous section, and it accounts for
the component c in equation (5).
Next, an iterative process is applied, in which the ith iteration
corresponds to a perturbation in the solution of the previous
iteration; the perturbation is formed by a linear combination
of the two basis functions of
order i (that is, i cycles). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
how the perturbations in the model are constructed for the first
two iterations. As explained in the figure caption, the actual
parameters to be estimated at each iteration are not a and b, but
dM1 and dM2, which are directly related to the perturbations
in each layer. Since we must consider perturbations in Mx as
well as in Mz, the number of independent parameters to be
estimated at each iteration will always be four:
dMx1, dMx2, dMz1, and dMz2.
shows
how the perturbations in the model are constructed for the first
two iterations. As explained in the figure caption, the actual
parameters to be estimated at each iteration are not a and b, but
dM1 and dM2, which are directly related to the perturbations
in each layer. Since we must consider perturbations in Mx as
well as in Mz, the number of independent parameters to be
estimated at each iteration will always be four:
dMx1, dMx2, dMz1, and dMz2.
Differently from the Fourier decomposition, here the number of points (layers) describing the model is not fixed for the retrieval of all the frequency components, but instead increases proportionally to the sequential number of the iteration. At each iteration, the total number of layers is four times the sequential number of the iteration. The solution is constructed in successive degrees of resolution, which results in a highly stable method, despite the use of a non-linear optimization algorithm.
The objective function to be minimized at each iteration is
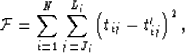 |
(6) |
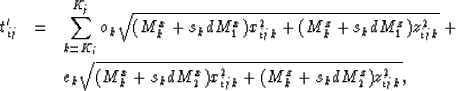 |
||
| (7) |
| |
(8) |
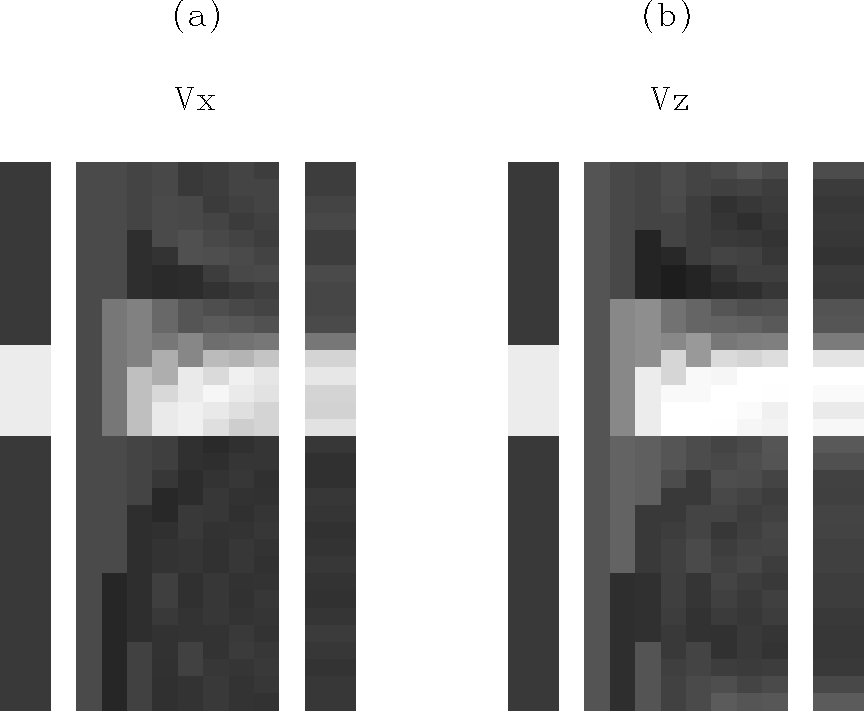
I applied the method to a synthetic dataset corresponding to a single isotropic horizontal layer immersed in an also isotropic background. The data consists of traveltimes from 20 shots localized in one well, each recorded by 51 receivers localized in the other well. The space between adjacent sources was 5 times as larger as the distance between adjacent receivers. The layer thickness and the distance between wells were 3.33 and 3.6 times the distance between sources, respectively. Figure 1 shows the original and the retrieved models, as well as the partial result of each iteration.
The final results for Vx and Vz are close enough to the original model, if we consider the resolution limit associated with the specific acquisition-parameters and geometry. As expected, the part of the model that corresponds to Vx converges faster, and for a better solution, than the part that corresponds to Vz. The layer thickness in the last iteration is about 3/5 the source interval.
 |