




Next: HORIZONTALLY LAYERED INVERSION
Up: Cunha: anisotropic traveltime inversion
Previous: Introduction
For elliptically anisotropic media, that is, media in which the group velocity
V has an elliptical dependence on the angle of energy propagation
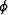 , such that
, such that
| 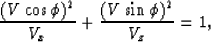 |
(1) |
the relation between group and phase velocities and angles is
given by a closed analytical form (Levin, 1978):
| 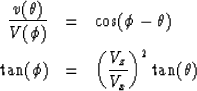 |
(2) |
| (3) |
where v and 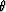 are the phase velocity and angle, respectively.
Equation ( 1) also represents an elliptical dispersion
relation, since
are the phase velocity and angle, respectively.
Equation ( 1) also represents an elliptical dispersion
relation, since 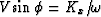 and
and
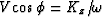 .It turns out that elasticity theory predicts this elliptical
dependence only for SH in a transverse isotropic symmetry, or
for all wave types in the trivial case of isotropic material where
the ellipse becomes a circle. However, the use of an elliptical
approximation for the dispersion relation can considerably simplify
the problem of estimating the elastic parameters from the recorded
wavefields.
.It turns out that elasticity theory predicts this elliptical
dependence only for SH in a transverse isotropic symmetry, or
for all wave types in the trivial case of isotropic material where
the ellipse becomes a circle. However, the use of an elliptical
approximation for the dispersion relation can considerably simplify
the problem of estimating the elastic parameters from the recorded
wavefields.
If we consider a source and a receiver separated by a vertical
distance z and a horizontal distance x, the
traveltime t predicted by equation (1) is
| 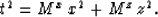 |
(4) |
The relation between the slownesses squared (or sloth) Mx and Mz
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) that best fits our data and the true vertical and horizontal sloths of
the medium Mv and Mh respectively will depend on the specific
geometry in which the data was collected. For an usual surface-seismic
geometry, equation (4) correspond to a paraxial approximation
around the vertical axis. In this case, Mx corresponds
to the estimated normal-moveout (NMO) sloth, while
that best fits our data and the true vertical and horizontal sloths of
the medium Mv and Mh respectively will depend on the specific
geometry in which the data was collected. For an usual surface-seismic
geometry, equation (4) correspond to a paraxial approximation
around the vertical axis. In this case, Mx corresponds
to the estimated normal-moveout (NMO) sloth, while 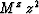 is the vertical traveltime. If z is unknown, then Mz
is an arbitrary factor that cannot be estimated (Dellinger and Muir, 1985).
is the vertical traveltime. If z is unknown, then Mz
is an arbitrary factor that cannot be estimated (Dellinger and Muir, 1985).
If both distances, x and z, are known
it is possible to estimate both sloth parameters by fitting the
data to equation (4). For surface seismic surveys the estimated
Mz will be close to the vertical sloth Mv, whereas for
a cross-well geometry the estimated Mx will be close to the
horizontal sloth Mh. Karrenbach (1989) described a scheme to
estimate these two sloth parameters using traveltime data from
the three wave types, for the case of a homogeneous medium.
He also derived the relations between these parameters and the
elastic constants corresponding to a transversely isotropic symmetry,
for the specific case of a cross-well geometry.





Next: HORIZONTALLY LAYERED INVERSION
Up: Cunha: anisotropic traveltime inversion
Previous: Introduction
Stanford Exploration Project
1/13/1998
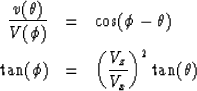
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) that best fits our data and the true vertical and horizontal sloths of
the medium Mv and Mh respectively will depend on the specific
geometry in which the data was collected. For an usual surface-seismic
geometry, equation (4) correspond to a paraxial approximation
around the vertical axis. In this case, Mx corresponds
to the estimated normal-moveout (NMO) sloth, while
that best fits our data and the true vertical and horizontal sloths of
the medium Mv and Mh respectively will depend on the specific
geometry in which the data was collected. For an usual surface-seismic
geometry, equation (4) correspond to a paraxial approximation
around the vertical axis. In this case, Mx corresponds
to the estimated normal-moveout (NMO) sloth, while