Next: SIMULTANEOUS ESTIMATION OF WAVELET
Up: DECONVOLUTION WITH A KNOWN
Previous: Building a more complex
Although I have not yet explored the practical implications of this,
the operator 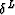 , previously defined, can be described
as a particular case of a more general operator
, previously defined, can be described
as a particular case of a more general operator 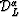 :
:
| 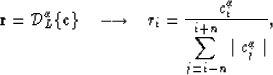 |
(10) |
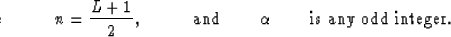
The operator 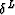 can be defined as
can be defined as
| 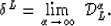 |
(11) |
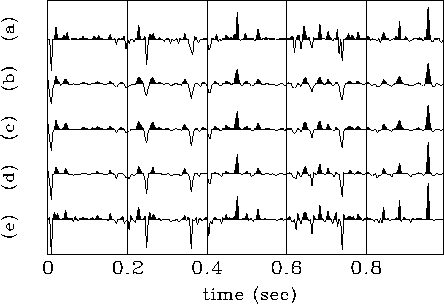
Figure 7 shows that using this operator
with finite values of  is equivalent to the introduction of
the damping factor in equation (7). Also we can see that
the results obtained with small values of
is equivalent to the introduction of
the damping factor in equation (7). Also we can see that
the results obtained with small values of  are
similar to those obtained with the predictive deconvolution.
An Lp norm deconvolution can be formulated as an iterative,
reweighted least-squares inversion with weighting factors given
by
are
similar to those obtained with the predictive deconvolution.
An Lp norm deconvolution can be formulated as an iterative,
reweighted least-squares inversion with weighting factors given
by 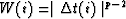 , where
, where 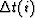 are the residuals of the previous iteration (Darche, 1989).
Since the value of the exponent
are the residuals of the previous iteration (Darche, 1989).
Since the value of the exponent
 will directly affect the relative weighting of the residuals,
we can consider the ICP decon as somehow equivalent to
an
will directly affect the relative weighting of the residuals,
we can consider the ICP decon as somehow equivalent to
an 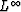 norm deconvolution.
norm deconvolution.
knowt3
Figure 7 (a) Original reflectivity series. The other traces
correspond to the results of the ICP algorithm using the
generalized operator of equation (10) with
different values of  : (b)
: (b) 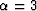 ,(c)
,(c) 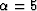 , (d)
, (d) 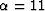 ,and (e)
,and (e) 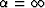 .
.






Next: SIMULTANEOUS ESTIMATION OF WAVELET
Up: DECONVOLUTION WITH A KNOWN
Previous: Building a more complex
Stanford Exploration Project
1/13/1998
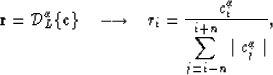
![]()
![]() is equivalent to the introduction of
the damping factor in equation (7). Also we can see that
the results obtained with small values of
is equivalent to the introduction of
the damping factor in equation (7). Also we can see that
the results obtained with small values of ![]() are
similar to those obtained with the predictive deconvolution.
An Lp norm deconvolution can be formulated as an iterative,
reweighted least-squares inversion with weighting factors given
by
are
similar to those obtained with the predictive deconvolution.
An Lp norm deconvolution can be formulated as an iterative,
reweighted least-squares inversion with weighting factors given
by ![]() , where
, where ![]() are the residuals of the previous iteration (Darche, 1989).
Since the value of the exponent
are the residuals of the previous iteration (Darche, 1989).
Since the value of the exponent
![]() will directly affect the relative weighting of the residuals,
we can consider the ICP decon as somehow equivalent to
an
will directly affect the relative weighting of the residuals,
we can consider the ICP decon as somehow equivalent to
an ![]() norm deconvolution.
norm deconvolution.