|
|
|
|
Tomographic full waveform inversion and linear modeling of multiple scattering |
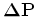 from the extended velocity.
It is performed by applying the adjoint
of the linear operator
from the extended velocity.
It is performed by applying the adjoint
of the linear operator
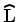 .
The application of
.
The application of
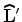 to the data residual is accomplished
similarly to the FWI gradient by
injecting the residual
at the receiver location and
running backward in time
the propagation expressed
in equation 17.
to the data residual is accomplished
similarly to the FWI gradient by
injecting the residual
at the receiver location and
running backward in time
the propagation expressed
in equation 17.
The third component
takes into account the dependency of
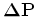 from the velocity at zero time lag;
its evaluation is more involved than for the previous two terms
but is crucial to the convergence of the inversion towards a velocity
model that explain the kinematics in the data.
The forward operator can be evaluated as a chain of two operators.
The first one relates perturbations in velocity to
perturbations in the background wavefield, as expressed
by equations 7-8.
The second one is computed by forward solving in time
equation 17, where the source term is given
by the perturbations in the background wavefield,
and not by the perturbations in the extended velocity.
Consequently this term is zero when the extended velocity
perturbations
from the velocity at zero time lag;
its evaluation is more involved than for the previous two terms
but is crucial to the convergence of the inversion towards a velocity
model that explain the kinematics in the data.
The forward operator can be evaluated as a chain of two operators.
The first one relates perturbations in velocity to
perturbations in the background wavefield, as expressed
by equations 7-8.
The second one is computed by forward solving in time
equation 17, where the source term is given
by the perturbations in the background wavefield,
and not by the perturbations in the extended velocity.
Consequently this term is zero when the extended velocity
perturbations
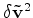 are zero,
independently from the perturbations in the background wavefield.
The adjoint is computed by applying the adjoint of these
two operators in reverse order.
are zero,
independently from the perturbations in the background wavefield.
The adjoint is computed by applying the adjoint of these
two operators in reverse order.
Finally, the gradient of the regularization terms depends on the expression
of the specific focusing operator 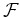 .
For the choice expressed in equation 23, the
computation of the gradient is trivial.
.
For the choice expressed in equation 23, the
computation of the gradient is trivial.
|
|
|
|
Tomographic full waveform inversion and linear modeling of multiple scattering |