|
|
|
|
Tomographic full waveform inversion and linear modeling of multiple scattering |
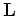 ,
which is the linearization of
,
which is the linearization of 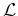 with respect to velocity perturbations
with respect to velocity perturbations
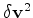 .
This linear operator can be derived by
perturbing equation 3 as follows
.
This linear operator can be derived by
perturbing equation 3 as follows
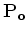 and
and
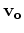 are the background wavefield
and velocity, respectively,
and
are the background wavefield
and velocity, respectively,
and
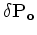 is the scattered wavefield.
is the scattered wavefield.
Equation 4 can be rewritten as the following
two equations:
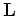 used to compute
the gradient of the FWI objective function 2
is evaluated by
recursively propagating the background wavefield
used to compute
the gradient of the FWI objective function 2
is evaluated by
recursively propagating the background wavefield
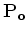 and the scattered wavefield
and the scattered wavefield
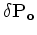 by solving equations 7-8.
by solving equations 7-8.
The scattered wavefield
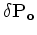 is a linear function of the velocity perturbations
is a linear function of the velocity perturbations
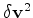 because equation 8 takes into account only
fist order scattering.
Notice that the linear operator
because equation 8 takes into account only
fist order scattering.
Notice that the linear operator
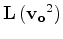 is itself a non linear function
of the background velocity, both directly by determining the
propagation speed of the scattered wavefield
(left hand side in equation 8),
and indirectly through the background wavefield
(right hand side in equation 8).
is itself a non linear function
of the background velocity, both directly by determining the
propagation speed of the scattered wavefield
(left hand side in equation 8),
and indirectly through the background wavefield
(right hand side in equation 8).
|
|
|
|
Tomographic full waveform inversion and linear modeling of multiple scattering |