Tomographic full waveform inversion and linear modeling of multiple scattering

Multiple-scattering modeling

We can achieve accurate modeling of perturbed wavefield by solving equations 5-6 instead of equations 7-8. Equations 5-6 can be solved numerically with a simple explicit method; that is, one that adds the scattered wavefield up to time 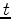${t}$ to the right-hand side of equation 6 to compute the scattered wavefield at ${t}+{\Delta{t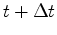}}$ . Even in presence of large velocity variations, the scattered wavefield has now the correct time shift. Numerical solutions produce accurate results, although the scattered wavefield is still propagated with the background velocity, because multiple scattering is taken into account of.

The challenge with using these equations in a gradient-based inversion algorithm is that the relation between the scattered wavefield 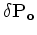${\bf {\delta P_o}}$ and the velocity perturbations 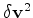$\delta{{\bf {v}}}^2$ is now nonlinear. In the next section, I present a method for linearizing this relation that is alternative to the conventional one represented by equations 7-8, and is based on an extension of the velocity model in time.

FWI-Norm-new Figure 1. FWI norm as a function of the true velocity, when the starting velocity is equal to 1.2 km/s.

FWI-Grad-new Figure 2. FWI search direction as a function of the true velocity, when the starting velocity is equal to 1.2 km/s.

Tomographic full waveform inversion and linear modeling of multiple scattering