Wave-equation tomography for anisotropic parameters

Conclusions and discussion

In this paper, we present a novel method to build the anisotropic velocity model using image-space wave-equation tomography. The mathematical formulation of the operator shows that by adding an additional term for 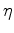$\eta$ , the gradient of the anisotropic WETom shows similar structure as that for the isotropic case. Our numerical tests show that the anisotropic WETom operator is useful in identifying both localized and layered perturbation in simple cases. However, when only one parameter is perturbed, the WETom operator produces a model with perturbations in both parameters.

One possible way to resolve this ambiguity is to utilize the moveout information in the subsurface offset domain and/or angle domain. It has been shown that the RMO functions are different in ADCIGs for isotropic perturbations (Biondi and Symes, 2004) and anisotropic perturbations (Biondi, 2007). Therefore, adding the RMO information may help to distinguish the contributions from different parameters. Also, data other than surface seismic data, such as well logs and checkshots, can also be helpful in further constraining the problem. This will be investigated in the near future.

Wave-equation tomography for anisotropic parameters