Generalized-norm conjugate direction solver

Solver internal mechanisms

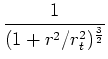In any optimization scheme, we always attempt to minimize some measure of a data or model residual, ${\bf r}$. This measure, $C({\bf r})$, is usually a convex function (commonly the $L_2$ norm, for least-squares fitting). For our solver, $C({\bf r})$ can be any of the norms listed in previous section. As proposed by Claerbout (2009), the numerical value of a norm at an updated residual value, $C({\bf r}_2)$ can be estimated based on a second-order Taylor series decomposition at point ${\bf r}_1$:

$$C({\bf r}_2) \approx C({\bf r}_1) + \frac{({\bf r}_2-{\bf r}_1)}{1!} C'({\bf r}_1) + \frac{({\bf r}_2-{\bf r} _1)^2}{2!} C''({\bf r}_1)$$ (13)

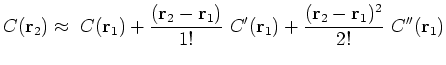where $r_2$ is the point in a close neighborhood of 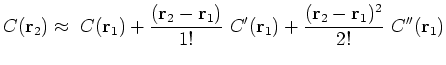$r_1$. With this generalization, we can conduct an iterative plane-search at any point $r_2$, without re-evaluating the forward operator. For operators with a high-op count per sample this is a less costly by finding a more optimal update to the solution.

Generalized-norm conjugate direction solver