Generalized-norm conjugate direction solver

Iterated Plane-Search

In the conjugate-direction descent (Claerbout, 2008), the update in the model and residual is defined by a linear combination of the current gradient of the objective function and the direction of the previous update step. However, this update can be iterated inside an inner loop, assuming a linearization of the gradient around the current residual. Our algorithm can perform an iterated search in the plane defined by the current gradient and the previous update step. This search can locate the optimal update without a full re-evaluation of the gradient operator. In practice, this is equivalent to finding the solution of a 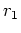$2\times2$ system of equations, where the unknowns are the step lengths in the direction of the gradient 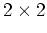${\bf g}^{(m)}$ and the previous step ${\bf s}^{(m)}$.

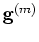Taylor series expansion of the objective function around the initial residual value, assumes a small local neighborhood for the plane-search. We re-calculate this approximation at every inner iteration; this is an essential element of the plane-search, to ensure a reasonable degree of accuracy without a full re-computation of the forward operator in the main body of solver.

Generalized-norm conjugate direction solver