




Next: About this document ...
Up: Tang: Imaging in the
Previous: acknowledgments
- Biondi, B. and G. Shan, 2002, Prestack imaging of overturned reflections by reverse time migration: 72nd Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 1284-1287.
-
- Biondi, B. and W. Symes, 2004, Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging: Geophysics, 69, 1283-1298.
-
- Howard, M. S. and N. Moldoveanu, 2006, Marine survey design for rich-azimuth seismic using surface streamers: 76rd Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 2915-2919.
-
- Keggin, J., T. Manning, et al., 2006, Key aspects of multi-azimuth acquisition and processing: 76rd Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 2886-2890.
-
- Michell, S., E. Shoshitaishvili, et al., 2006, Wide azimuth streamer imaging of mad dog: Have we solved the subsalt imaging problem?: 76rd Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 2905-2909.
-
- Mosher, C. and D. Foster, 2000, Common angle imaging conditions for prestack depth migration: 70th Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 830-833.
-
- Prucha, B. B., M. and W. Symes, 1999, Angle-domain common image gathers by wave-equation migration: 69th Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 824-827.
-
- Prucha, M. L., R. G. Clapp, and B. Biondi, 2000, Seismic image regularization in the reflection angle domain: SEP-103, 109-119.
-
- Rickett, J. E. and P. C. Sava, 2002, Offset and angle-domain common image-point gathers for shot-profile migration: Geophysics, 67, 883-889.
-
- Sava, P. C. and S. Fomel, 2003, Angle-domain common-image gathers by wavefield continuation methods: Geophysics, 68, 1065-1074.
-
- Soubaras, R., 2003, Angle gathers for shot-record migration by local harmonic decomposition: 73rd Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 889-892.
-
- Tang, Y., 2006, Least-squares migration of incomplete data sets with regularization in the subsurface-offset domain:, SEP-125, 159-174.
-
- Tisserant, T. and B. Biondi, 2003, Wavefield-continuation angle-domain common-image gathers in 3-D: SEP-113, 211-220.
-
- Valenciano, A. A. and B. Biondi, 2004, Target-oriented computation of the wave-equation imaging Hessian: SEP-117, 63-76.
-
- Valenciano, A. A., 2006, Target-oriented wave-equation inversion with regularization in the subsurface offset domain: SEP-124.
-
- Xie, X. and R. Wu, 2002, Extracting angle domain information from migrated wavefield: 72nd Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 1360-1363.
-
A
This appendix analytically derives SODCIGs for one shot and well-sampled receiver wavefields in
locally constant-velocity media. Let's consider the SODCIG for a dipping reflector
at image point (xm, zm), as shown in Figure (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The dipping angle is
). The dipping angle is 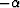 , while the reflection
angle at (xm, zm) is
, while the reflection
angle at (xm, zm) is 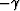 (assuming positive sign for angles measured in a clockwise direction).
The red circle shows the source wavefront at some time t, which intersects the dipping reflector
at (xm, zm). If we put receivers
for every location on the surface, i.e. the receiver wavefield is sufficiently densely sampled, when we downward continue or
backward propagate the receiver wavefield, the circular wavefront, which is in blue, can be well reconstructed. It also intersets
the dipping reflector at (xm, zm) at the same time t. Therefore, cross-correlation of the source wavefield and receiver
wavefield will generate the image at (xm, zm).
(assuming positive sign for angles measured in a clockwise direction).
The red circle shows the source wavefront at some time t, which intersects the dipping reflector
at (xm, zm). If we put receivers
for every location on the surface, i.e. the receiver wavefield is sufficiently densely sampled, when we downward continue or
backward propagate the receiver wavefield, the circular wavefront, which is in blue, can be well reconstructed. It also intersets
the dipping reflector at (xm, zm) at the same time t. Therefore, cross-correlation of the source wavefield and receiver
wavefield will generate the image at (xm, zm).
dip.full.rec
Figure 14 When the receiver wavefield is sufficiently densely sampled,
the actual circular wavefront in blue can be well reconstructed.
|
|  |

The equation for the source wavefront in red is
| ![\begin{displaymath}
\left( x-s \right)^2 + z^2 = \left[\frac{(x_m-s)}{\sin(-\gamma+\alpha)}\right]^2,\end{displaymath}](img17.gif) |
(8) |
while the equation for the receiver wavefront in blue is
| ![\begin{displaymath}
\left[x-s\cos(-2\alpha)\right]^2 + \left[z-s\sin(-2\alpha)\right]^2 = \left[\frac{(x_m-s)}{\sin(-\gamma+\alpha)}\right]^2.\end{displaymath}](img18.gif) |
(9) |
To get the local offset gather at xm, we have to apply the multi-offset imaging condition described in equation (1)
as follows, where h is the subsurface half-offset.
| ![\begin{displaymath}
\left\{\begin{array}
{l}
\left( x-h-s \right)^2 + z^2 = \le...
...rac{(x_m-s)}{\sin(-\gamma+\alpha)}\right]^2
\end{array}\right.\end{displaymath}](img19.gif) |
(10) |
Therefore, by letting x=xm and subtracting the second equation from the first equation, we get
| ![\begin{displaymath}
\left( x_m-h-s \right)^2 + z^2 = \left[x_m+h-s\cos(-2\alpha)\right]^2 + \left[z-s\sin(-2\alpha)\right]^2.\end{displaymath}](img20.gif) |
(11) |
After some algebra, we get
| ![\begin{displaymath}
\left[2x_m-s(1+\cos(-2\alpha))\right]\left[s(\cos(-2\alpha)-1)-2h\right] + (2z-s\sin(-2\alpha))s\sin(-2\alpha) = 0.\end{displaymath}](img21.gif) |
(12) |
Rearranging the above equation:
| 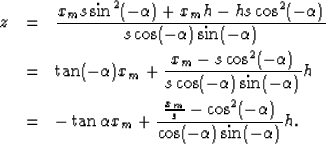 |
(13) |
| (14) |
| (15) |
From Figure (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), point (xm,zm) on the dipping reflector satisfies:
), point (xm,zm) on the dipping reflector satisfies:
| 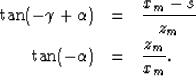 |
(16) |
| (17) |
Multiplying them together yields
| 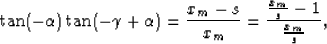 |
(18) |
so
| 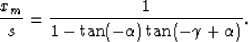 |
(19) |
Substituting equation(19) into equation (15), we get:
| 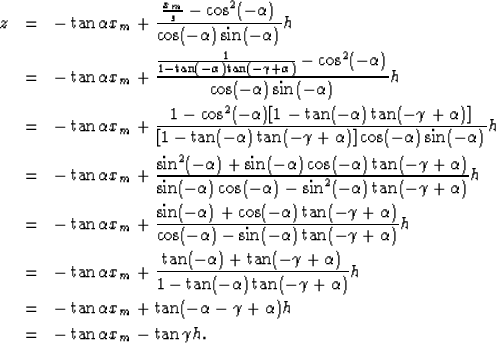 |
(20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
Actually the above equation is true for each point (x,z) with dipping angle  and opening angle
and opening angle 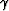 , so it can be
rewritten as follows:
, so it can be
rewritten as follows:
| 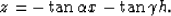 |
(28) |
Therefore, when the receiver wavefield is sufficiently densely sampled, the SODCIG is linearly related to the
angle gather.
B
This appendix analytically derives SODCIGs for one shot and one receiver in locally constant-velocity media.
Let's again consider a dipping reflector with the dip angle  , as shown in Figure
, as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The
source is located at (s,0), while receiver is located at (r,0). Since there is only one receiver, when we downward continue
or backward propagate the receiver wavefield, the receiver wavefront that intersects (xm, zm)
is the green one shown in Figure
. The
source is located at (s,0), while receiver is located at (r,0). Since there is only one receiver, when we downward continue
or backward propagate the receiver wavefield, the receiver wavefront that intersects (xm, zm)
is the green one shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) instead of the blue one shown in Figure
instead of the blue one shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
dip.one.rec
Figure 15 In the extreme situation where there is only one receiver,
the receiver wavefront is the one shown here in green, instead of the blue one
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . .
|
|  |

The image point at (xm, zm) on the dipping reflector certainly satisfies:
| 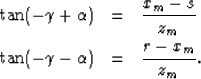 |
(29) |
| (30) |
Thus, we have:
| 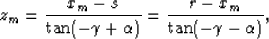 |
(31) |
which rearranges to
| 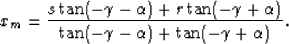 |
(32) |
Since (xm, zm) is the intersecting point of the source wavefront and the receiver wavefront, it should satisfy the source wavefront equation:
| ![\begin{displaymath}
\left( x-s \right)^2 + z^2 = \left[\frac{x_m-s}{\sin(-\gamma+\alpha)}\right]^2,\end{displaymath}](img31.gif) |
(33) |
and the receiver wavefront equation:
| ![\begin{displaymath}
\left( x-r \right)^2 + z^2 = \left[\frac{r-x_m}{\sin(-\gamma-\alpha)}\right]^2.\end{displaymath}](img32.gif) |
(34) |
To get the SODCIG, we have to apply the multi-offset imaging conditon
described in equation (1) as follows, where h is the subsurface half-offset,
| ![\begin{displaymath}
\left\{\begin{array}
{l}
\left( x-h-s \right)^2 + z^2 = \lef...
...frac{(x_m-r)}{\sin(-\gamma-\alpha)}\right]^2.\end{array}\right.\end{displaymath}](img33.gif) |
(35) |
Therefore, by letting x=xm and summing the above two equations together, we can derive the relationship between z and h for surface location xm:
| ![\begin{displaymath}
(x_m-h-s)^2 + (x_m+h-r)^2 + 2z^2 = \left[\frac{x_m-s}{\sin(-...
...)}\right]^2 + \left[\frac{r-x_m}{\sin(-\gamma-\alpha)}\right]^2\end{displaymath}](img34.gif) |
(36) |
From equation (32), it is easy to get:
| 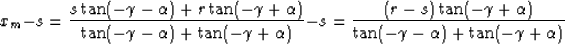 |
(37) |
and
| 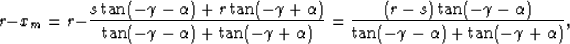 |
(38) |
Substituting equations (37) and (38) into equation (36), after some algebra, we get
| ![\begin{displaymath}
z^2 = -h^2 + (r-s)h+\frac{(r-s)^2}{\left[\tan(-\gamma -\alpha) + \tan(-\gamma+\alpha)\right]^2}.\end{displaymath}](img37.gif) |
(39) |
Obviously, in this situation, depth z is not linearly related to subsurface half-offset h. When 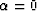 , i.e. for a flat reflector,
the above equation can be simplified as follows:
, i.e. for a flat reflector,
the above equation can be simplified as follows:
| 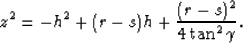 |
(40) |





Next: About this document ...
Up: Tang: Imaging in the
Previous: acknowledgments
Stanford Exploration Project
5/6/2007
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The dipping angle is
). The dipping angle is ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The dipping angle is
). The dipping angle is ![]() , while the reflection
angle at (xm, zm) is
, while the reflection
angle at (xm, zm) is ![]() (assuming positive sign for angles measured in a clockwise direction).
The red circle shows the source wavefront at some time t, which intersects the dipping reflector
at (xm, zm). If we put receivers
for every location on the surface, i.e. the receiver wavefield is sufficiently densely sampled, when we downward continue or
backward propagate the receiver wavefield, the circular wavefront, which is in blue, can be well reconstructed. It also intersets
the dipping reflector at (xm, zm) at the same time t. Therefore, cross-correlation of the source wavefield and receiver
wavefield will generate the image at (xm, zm).
(assuming positive sign for angles measured in a clockwise direction).
The red circle shows the source wavefront at some time t, which intersects the dipping reflector
at (xm, zm). If we put receivers
for every location on the surface, i.e. the receiver wavefield is sufficiently densely sampled, when we downward continue or
backward propagate the receiver wavefield, the circular wavefront, which is in blue, can be well reconstructed. It also intersets
the dipping reflector at (xm, zm) at the same time t. Therefore, cross-correlation of the source wavefield and receiver
wavefield will generate the image at (xm, zm).

![\begin{displaymath}
\left\{\begin{array}
{l}
\left( x-h-s \right)^2 + z^2 = \le...
...rac{(x_m-s)}{\sin(-\gamma+\alpha)}\right]^2
\end{array}\right.\end{displaymath}](img19.gif)
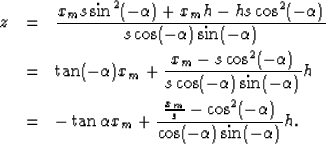
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), point (xm,zm) on the dipping reflector satisfies:
), point (xm,zm) on the dipping reflector satisfies:
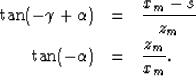
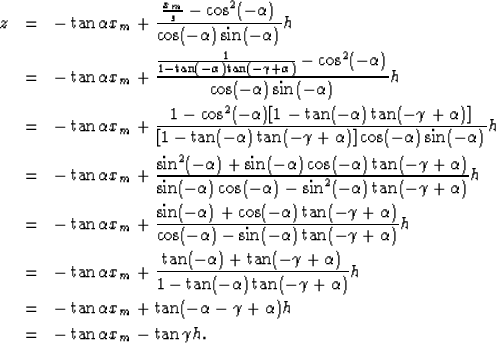
![]() , as shown in Figure
, as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The
source is located at (s,0), while receiver is located at (r,0). Since there is only one receiver, when we downward continue
or backward propagate the receiver wavefield, the receiver wavefront that intersects (xm, zm)
is the green one shown in Figure
. The
source is located at (s,0), while receiver is located at (r,0). Since there is only one receiver, when we downward continue
or backward propagate the receiver wavefield, the receiver wavefront that intersects (xm, zm)
is the green one shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) instead of the blue one shown in Figure
instead of the blue one shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

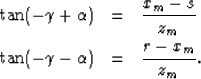
![\begin{displaymath}
\left\{\begin{array}
{l}
\left( x-h-s \right)^2 + z^2 = \lef...
...frac{(x_m-r)}{\sin(-\gamma-\alpha)}\right]^2.\end{array}\right.\end{displaymath}](img33.gif)